المعادلات التربيعية (كاملة): التعريف ، الصيغ ، مثال على المشاكل

المعادلة التربيعية هي إحدى المعادلات الرياضية للمتغير الذي لديه أعلى قوة من اثنين.

الشكل العام للمعادلة التربيعية أو PK هو كما يلي:

الفأس 2 + ب س + ج = 0

حيث x هو المتغير ، و a ، و b هو المعامل ، و c هو الثابت. قيمة a لا تساوي الصفر.

أشكال الرسم البياني

إذا تم وصف معادلة تربيعية من حيث الإحداثيات الديكارتية (س ، ص) ، فإنها تشكل رسمًا بيانيًا مكافئًا. لذلك غالبًا ما يشار إلى المعادلات التربيعية باسم المعادلات المكافئة .

فيما يلي مثال على شكل هذه المعادلة في شكل رسم بياني مكافئ.

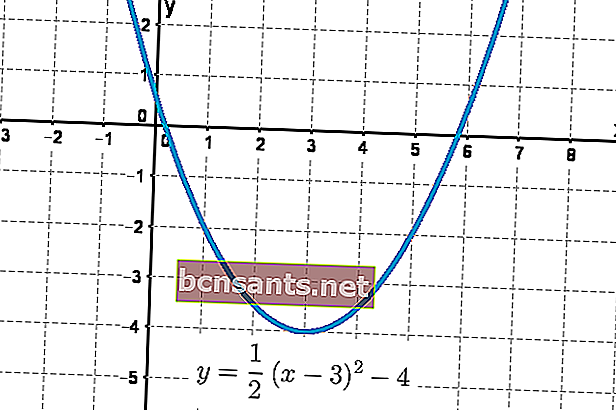
في المعادلة العامة ، تؤثر القيم a و b و c بشكل كبير على نمط القطع المكافئ الناتج.

تحدد قيمة a المنحنى المقعر أو المحدب للقطع المكافئ. إذا كانت القيمة > 0 ، فسيتم فتح القطع المكافئ (مقعر) . على العكس من ذلك ، إذا كانت القيمة <0 ، فسيتم فتح القطع المكافئ لأسفل (محدب) .

تحدد قيمة b في المعادلة رأس القطع المكافئ . بمعنى آخر ، حدد قيمة محور تناظر المنحنى والتي تساوي x = - b / 2a .

تحدد القيمة الثابتة c على الرسم البياني للمعادلة نقطة تقاطع دالة القطع المكافئ على المحور y . التالي هو رسم بياني قطع مكافئ مع التغيرات في القيمة الثابتة ج .

جذور المعادلة التربيعية (PK)

يسمى حل المعادلة التربيعية كار - جذر المعادلة التربيعية .

جذور قتل مختلفة

يمكن إيجاد أنواع الجذور PK بسهولة باستخدام الصيغة العامة D = b2 - 4ac من المعادلة العامة للمحور التربيعي 2 + bx + c = 0

فيما يلي أنواع جذور المعادلات التربيعية.

1. الجذر الحقيقي (D> 0)

إذا كانت قيمة D> 0 من PK ، فستنتج جذورًا حقيقية ولكن لها جذور مختلفة. بمعنى آخر ، x1 ليس هو نفسه x2.

مثال على معادلة الجذر الحقيقية (D> 0)

أوجد نوع جذر المعادلة x2 + 4x + 2 = 0.

المحلول:

أ = 1 ؛ ب = 4 ؛ و ج = 2

د = ب 2 - 4 أ

د = 42-4 (1) (2)

د = 16-8

د = 8

بما أن قيمة D> 0 ، فإن الجذر من نوع الجذر الحقيقي.

2- الجذر الحقيقي يساوي x1 = x2 (D = 0)

هو نوع من جذر المعادلة التربيعية التي تنتج جذورًا بنفس القيمة (x1 = x2).

مثال على الجذور الحقيقية (D = 0)

أوجد قيمة جذر PK لـ 2x2 + 4x + 2 = 0.

اقرأ أيضًا: أنواع دورات المياه (+ الصورة الكاملة والشرح)

المحلول:

أ = 2 ؛ ب = 4 ؛ ج = 2

د = ب 2 - 4 أ

د = 42-4 (2) (2)

د = 16-16

د = 0

لذلك ، نظرًا لأن قيمة D = 0 ، فقد ثبت أن الجذور حقيقية ومتزاوجة.

3. جذور خيالية / ليست حقيقية (D <0)

إذا كانت قيمة D <0 ، فإن جذر المعادلة التربيعية سيكون تخيليًا / غير حقيقي.

مثال على الجذور التخيلية (D <0) /

أوجد نوع جذر المعادلة x2 + 2x + 4 = 0.

المحلول:

أ = 1 ؛ ب = 2 ؛ ج = 4

د = ب 2 - 4 أ

د = 22-4 (1) (4)

د = 4-16

د = -12

لذا بما أن قيمة D <0 ، فإن جذر المعادلة هو جذر غير واقعي أو وهمي.

أوجد جذور المعادلة التربيعية

هناك عدة طرق يمكن استخدامها لإيجاد جذور المعادلة التربيعية. من بينها العوامل والمربعات الكاملة واستخدام الصيغة abc.

فيما يلي وصف لعدة طرق لإيجاد جذور المعادلة.

1. التخصيم

التخصيم / التحليل هو طريقة لإيجاد الجذور من خلال البحث عن القيمة التي ، إذا تضاعفت ، ستنتج قيمة أخرى.

هناك ثلاثة أشكال من المعادلات التربيعية (PK) بعوامل جذر مختلفة ، وهي:

لا.	شكل المعادلة	عامل الجذر
1	س 2 + 2 س ص + ص 2 = 0	(س + ص) 2 = 0
2	س 2 - 2 س ص + ص 2 = 0	(س - ص) 2 = 0
3	س 2 - ص 2 = 0	(س + ص) (س - ص) = 0

فيما يلي مثال لمشكلة تتعلق باستخدام طريقة التحليل في المعادلات التربيعية.

حل المعادلة التربيعية 5x 2 + 13x + 6 = 0 باستخدام طريقة التحليل.

المحلول:

5 س 2 + 13 س = 6 = 0

5 س 2 + 10 س + 3 س + 6 = 0

5 س (س + 2) + 3 (س + 2) = 0

(5 س + 3) (س + 2) = 0

5 س = -3 أو س = -2

إذن ، سيكون الحل هو x = -3/5 أو x = -2

2. المربعات المثالية

في الدرجة الثانية مثالية النموذج هو معادلة من الدرجة الثانية التي تنتج الأرقام عقلانية .

تستخدم نتائج المعادلة التربيعية المثالية بشكل عام الصيغة التالية:

(س + ع) 2 = س 2 + 2 بكسل + ع 2

الحل العام للمعادلة التربيعية المثالية هو كما يلي:

(س + ع) 2 = س 2 + 2 بكسل + ع 2

مع (x + p) 2 = q ، ثم:

(س + ع) 2 = ف

س + ص = ± س

س = -p ± q

فيما يلي مثال لمشكلة تتعلق باستخدام طريقة المعادلة المثالية.

حل المعادلة x2 + 6x + 5 = 0 باستخدام طريقة المعادلة التربيعية المثالية!

المحلول:

س 2 + 6 س +5 = 0

س 2 + 6 س = -5

الخطوة التالية هي إضافة رقم واحد على الجانبين الأيمن والأيسر بحيث يمكن تغييره إلى مربع كامل.

س 2 + 6 س + 9 = -5 + 9

س 2 + 6 س + 9 = 4

(س + 3) 2 = 4

(س + 3) = -4

س = 3 ± 2

إذن ، النتيجة النهائية هي x = -1 أو x = -5

اقرأ أيضًا: تعريف واختلاف المرادفات المتجانسة والمتجانسات والمتجانسات

3. صيغ ABC التربيعية

صيغة abc هي خيار بديل عندما لا يمكن حل المعادلة التربيعية عن طريق التحليل إلى عوامل أو طرق تربيعية مثالية.

فيما يلي صيغة abc للمعادلة التربيعية ax2 + bx + c = 0.

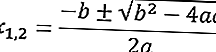
فيما يلي مثال لحل مشكلة معادلة من الدرجة الثانية باستخدام صيغة abc .

حل المعادلة x2 + 4x - 12 = 0 باستخدام طريقة صيغة abc!

المحلول:

x2 + 4x - 12 = 0

حيث أ = 1 ، ب = 4 ، ج = -12

بناء معادلة تربيعية جديدة

إذا تعلمنا سابقًا كيفية العثور على جذور المعادلة ، فسنتعلم الآن كيفية تكوين المعادلة التربيعية من الجذور التي كانت معروفة سابقًا.

فيما يلي بعض الطرق التي يمكنك من خلالها بناء PK جديد.

1. بناء المعادلات عندما تعرف الجذور

إذا كانت المعادلة لها جذور x1 و x2 ، فيمكن التعبير عن معادلة هذين الجذور بدلالة

(x- x ₁ ) (x- x ₂ ) = 0

مثال:

أوجد معادلة تربيعية حيث الجذور بين -2 و 3.

المحلول:

س ₁ = -2 و س ₂ = 3

(س - (- 2)) (س -3) = 0

(س + 2) (س + 3)

x2-3x + 2x-6 = 0

x2-x-6 = 0

إذن ، نتيجة معادلة هذين الجذور هي x2-x-6 = 0

2. كوّن معادلة تربيعية إذا كنت تعرف عدد الجذور وحاصل ضربها

إذا كانت جذور المعادلة التربيعية مع عدد وأوقات x1 و x2 معروفة ، فيمكن تحويل المعادلة التربيعية إلى الشكل التالي.

x2- (x ₁₊ x ₂ ) x + (x _1. x ₂ ) = 0

مثال:

أوجد معادلة تربيعية بالجذور 3 و 1/2.

المحلول:

x ₁ = 3 و x ₂ = -1/2

× ₁₊ × ₂ = 3-1/2 = 6/2 - 1/2 = 5/2

× _1. × ₂ = 3 (-1/2) = -3/2

وبالتالي ، فإن المعادلة التربيعية هي:

x2- (x ₁₊ x ₂ ) x + (x _1. x ₂ ) = 0

x2-5 / 2 x - 3/2 = 0 (كل جانب مضروب في 2)

2x2-5x-3 = 0

إذن ، المعادلة التربيعية للجذور 3 و 1/2 هي 2x2-5x-3 = 0.