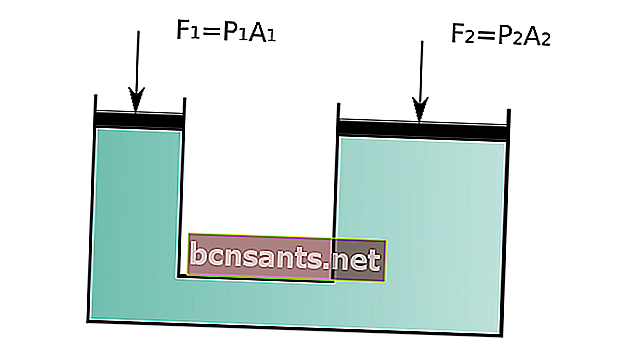
يقرأ قانون باسكال: "إذا تم تطبيق ضغط خارجي على نظام مغلق ، فإن الضغط في أي نقطة في السائل سيزداد بما يتناسب مع الضغط الخارجي المطبق".
هل سبق لك أن رأيت محل تصليح يغير الإطارات؟ إذا كان الأمر كذلك ، فمن المؤكد أنك سترى أن السيارة أو حتى الشاحنة يتم رفعها أولاً باستخدام أداة صغيرة تسمى الرافعة.
بالطبع السؤال الذي يطرح نفسه هو كيف يمكن للرافعة أن ترفع سيارة تزن آلاف المرات من الرافعة.

يتم شرح الإجابة على هذا السؤال من خلال قانون يسمى قانون باسكال. لمزيد من التفاصيل ، دعنا نلقي نظرة أكثر على قانون باسكال مع مثال على المشكلة.
فهم قانون باسكال
في القرن السادس عشر ، صاغ الفيلسوف والعالم بليز باسكال قانونًا يسمى قانون باسكال. يقرأ هذا القانون:
"إذا تم تطبيق ضغط خارجي على نظام مغلق ، فإن الضغط في أي نقطة في السائل سيزداد بما يتناسب مع الضغط الخارجي المطبق."
العلم الأساسي لهذا القانون هو الضغط ، حيث يكون الضغط المطبق على السائل بنظام مغلق مساويًا للضغط الخارج من النظام.
بفضله ، بدأت الابتكارات في الظهور ، خاصة للتغلب على مشكلة رفع الأحمال الثقيلة. ومن الأمثلة على ذلك الرافعات والمضخات والأنظمة الهيدروليكية في الكبح.
معادلة
قبل الانتقال إلى معادلة أو صيغة قانون باسكال ، نحتاج إلى تعلم العلوم الأساسية ، أي الضغط. التعريف العام للضغط هو التأثير أو القوة المؤثرة على السطح. الصيغة العامة للمعادلة هي:
P = F / A
أين :
P هو الضغط (Pa)
F هي القوة (N)
أ هي مساحة السطح الفعالة (م 2)
المعادلة الرياضية لقانون باسكال بسيطة للغاية حيث:
اقرأ أيضًا: التركيب البكتيري والوظيفة والصور [كاملة]أدخل = خروج
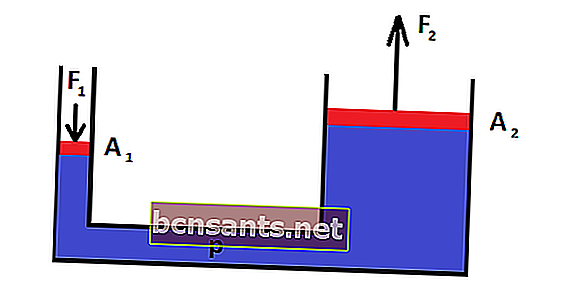
بالصورة أعلاه ، يمكن كتابة معادلة قانون باسكال على النحو التالي:
P1 = P2
F1 / A1 = F2 / A2
مع:
P1: ضغط المدخل (Pa)
P2: ضغط المخرج (Pa)
F1: القوة المطبقة (N)
F2: القوة المنتجة (N)
A1: منطقة القوة المطبقة (م 2)
A2: المساحة الناتجة (م 2)
بالإضافة إلى ذلك ، هناك مصطلح آخر يستخدم في تطبيق قانون باسكال والذي يشار إليه بالميزة الميكانيكية. بشكل عام ، الميزة الميكانيكية هي النسبة بين القوة التي يمكن أن ينتجها النظام والقوة التي يجب تطبيقها. رياضيا ، يمكن كتابة الميزة الميكانيكية:
الميزة الميكانيكية = F2 / F1
كما في مثال رافع السيارة الهيدروليكي ، سيكون للسائل الموجود في النظام نفس الحجم دائمًا.

لذلك ، يمكن أيضًا كتابة معادلة قانون باسكال كنسبة حجم داخل وخارج والتي:
V1 = V2
أو يمكن كتابتها كـ
A1.h1 = A2.h2
أين :
V1 = الحجم المدفوع
V2 = الحجم الذي يخرج
A1 = منطقة قسم الدخول
A2 = منطقة الخروج
h1 = عمق القسم الوارد
h2 = ارتفاع قسم الخروج
مثال على المشاكل
فيما يلي بعض الأمثلة ومناقشة الأسئلة من تطبيق قانون باسكال حتى تتمكن من الفهم بسهولة أكبر.
مثال 1
تستخدم رافعة هيدروليكية لرفع حمولة 1 طن. إذا كانت النسبة بين مساحة المقطع العرضي 1: 200 ، فما أقل قوة يجب أن تطبق على الرافعة الهيدروليكية؟
إجابة:
A1 / A2 = 1: 200
م = 1000 كجم ، ثم W = م. ز = 1000. 10 = 10000 شمال
F1 / A1 = F2 / A2
F1 / F2 = A1 / A2
F1 / 10000 = 1/200
F1 = 50 نيوتن
إذن القوة التي يتعين على النظام القيام بها هي 50 نيوتن
مثال 2
تبلغ قيمة الميزة الميكانيكية للرافعة الهيدروليكية 20. إذا أراد شخص ما رفع سيارة تزن 879 كجم ، فما القوة التي يجب أن يفعلها النظام؟
إجابة:
م = 879 كجم ، ثم W = مجم = 879. 10 = 8790 شمالاً
الكسب الميكانيكي = 20
F2 / F1 = 20
8790 / F1 = 20
F1 = 439.5 نيوتن
لذا فإن القوة المؤثرة على الرافعة المالية هي 439.5 نيوتن
اقرأ أيضًا: 1 سنة كم عدد الأسابيع؟ (من سنوات إلى أسابيع) إليكم الجوابمثال 3
رافعة هيدروليكية لها مكبس مدخل بقطر 14 سم وقطر مخرج 42 سم. إذا نزل المكبس إلى عمق 10 سم ، فما ارتفاع المكبس المرفوع؟
إجابة:
للمكبس سطح دائري لذا مساحته
A1 = π. r12 = 22/7. (14/2) 2 = 154 سم 2
A2 = π. r22 = 22/7. (42/2) 2 = 1386 سم 2
h1 = 10 سم
ثم
أ 1. h1 = A2. h2
154. 10 = 1386. h2
م 2 = 1540/1386
h2 = 1.11 سم
لذا فإن المكبس المرفوع يبلغ ارتفاعه 1.11 سم
مثال 4
يبلغ قطر الضاغط المزود بخرطوم متصل بصنبور 14 ملم. إذا تم تركيب بخاخ بفوهة 0.42 مم في نهاية الخرطوم وعند تشغيل الضاغط ، يتم قياس الضغط عند 10 بار. حدد مقدار قوة عادم الهواء التي تخرج من الفوهة إذا لم ينخفض ضغط الضاغط.
الجواب :
تحتوي الخراطيم والثقوب على منطقة مستعرضة دائرية
ثم مساحة سطح الحفرة
A2 = π. r22 = 22/7. (1،4 / 2) 2 = 1.54 ملم 2
"تذكر أن قانون باسكال يوضح أن الضغط في الداخل يساوي الضغط الخارج."
بحيث تكون القوة الجوية المنتهية ولايتها:
P = F / A
F = P. أ
F = 10 بار. 1.54 مم 2
قم بتغيير شريط الوحدة إلى باسكال و mm2 إلى m2
ثم
F = 106 باسكال. 1.54 × 10-6 م 2
القوة = 1.54 نيوتن
إذن قوة الرياح الخارجة هي 1.54 نيوتن
وبالتالي فإن المناقشة حول قانون باسكال ، نأمل أن تكون مفيدة لك.
