
التكامل غير المحدد أو المعروف أيضًا باسم مضاد الاشتقاق هو شكل من أشكال عملية التكامل التي تنتج وظيفة جديدة .
يلعب Integral دورًا مهمًا جدًا في الرياضيات. يمكن للنظرية تحديد المنطقة الواقعة تحت منحنى الوظيفة.
التكامل مفيد لحد المجموع المستمر على دالة متصلة. Integral هو مضاد مشتق. بعد ذلك ، إذا كانت f دالة متصلة ، فسيتم الإشارة إلى النتيجة المتكاملة للدالة f .
أنواع Intergral القائمة على حدود وظيفية معينة ليست مؤكدة. فيما يلي مناقشة لأنواع التكاملات ذات الحدود غير المحددة.
لا يتجزأ إلى أجل غير مسمى
التكامل غير المحدد أو المعروف أيضًا باسم مضاد الاشتقاق أو مضاد التباعد هو شكل من أشكال عملية التكامل التي تنتج وظيفة جديدة.
تأمل المعادلة التالية.

مع C ثابت. الصيغة المتكاملة لأجل غير مسمى هي كما يلي
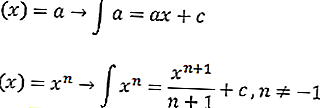
أو يساوي

مع
- أ (س) ^ ن = دالة المعادلة
- أ = ثابت
- س = متغير
- ن = قوة دالة المعادلة
- C = ثابت
نتيجة هذا التكامل غير المحدد هي وظيفة جديدة ليس لها قيمة معينة أو محددة لأنه لا تزال هناك متغيرات في الوظيفة الجديدة.
لكي تفهم بشكل أفضل مفهوم التكامل غير المحدد ، فكر في المثال أدناه.

بناءً على هذا المثال ، يمكن صياغة عملية متكاملة ، وهي
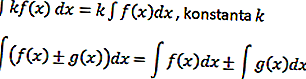
لا يتجزأ المثلثية
لا يعتبر تكامل الدالة بالضرورة ثابتًا أو خطيًا أو متعدد الحدود. في هذا الحل بين الأجيال ، غالبًا ما يتضمن العناصر المثلثية.
في الدالة المثلثية ، تنطبق أيضًا تعريفات التكاملات المرتبة في الجدول التالي.
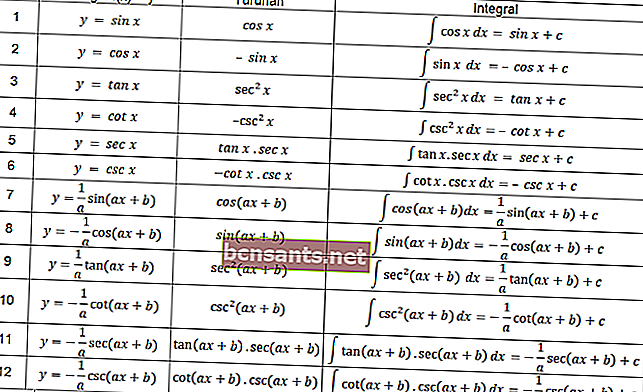
يمكنك استخدام المعادلات في الجدول أعلاه لحل مشكلة تكاملية تتضمن حساب المثلثات.
لفهم التكاملات المثلثية بشكل أفضل ، يمكنك فهم الأمثلة التالية
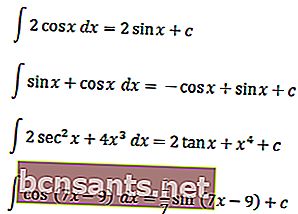
كان هذا هو تفسير التكاملات غير المحددة في التوابع المثلثية العادية والخاصة. نأمل أن تتم دراستها جيدًا.
اقرأ أيضًا: قواعد الحشمة: التعريف والغرض والعقوبات والأمثلة [كاملة]من أجل فهم مفهوم هذا التكامل بشكل أفضل ، يمكنك التدرب على إجراء أسئلة تدريبية. إذا كان هناك شيء تريد طرحه ، فقم بتدوينه في عمود التعليقات.
