معادلات الدائرة - الصيغ والنماذج العامة وأمثلة المسائل

معادلة الدائرة لها الصيغة العامة x ^ 2 + y ^ 2 + Ax + By + C = 0 ، والتي يمكن استخدامها لتحديد نصف قطر ومركز الدائرة.

تحتوي معادلة الدائرة التي ستتعلمها أدناه على عدة أشكال. في حالات مختلفة ، يمكن أن تكون المعادلة مختلفة. لذلك افهمها جيدًا حتى تتمكن من حفظها عن ظهر قلب.

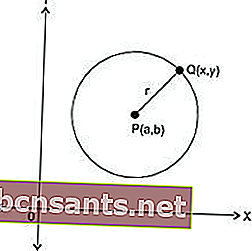
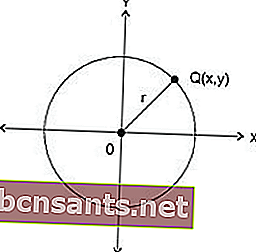
الدائرة هي مجموعة من النقاط التي تكون على مسافة متساوية من نقطة. يتم تحديد إحداثيات هذه النقاط من خلال ترتيب المعادلات. يتم تحديد ذلك بناءً على طول نصف القطر وإحداثيات مركز الدائرة.

معادلات الدائرة

هناك أنواع مختلفة من المعادلات ، وهي المعادلات المكونة من نقطة المركز ونصف القطر والمعادلة التي يمكن إيجادها لنقطة المركز ونصف القطر.

معادلة الدائرة العامة

توجد معادلة عامة على النحو التالي:

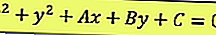
انطلاقا من المعادلة أعلاه ، يمكن تحديد نقطة المركز ونصف القطر ، وهما:

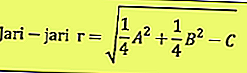
مركز الدائرة هو:

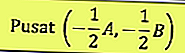
في مركز P (أ ، ب) ونصف القطر ص

من دائرة ، إذا كنت تعرف نقطة المركز ونصف القطر ، فستحصل على الصيغة:

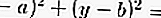
إذا كنت تعرف النقطة المركزية لدائرة ونصف قطر الدائرة حيث (أ ، ب) هو المركز وص هو نصف قطر الدائرة.

من المعادلة التي تم الحصول عليها أعلاه ، يمكننا تحديد ما إذا كان تضمين النقطة يقع على الدائرة ، أو في الداخل أو الخارج. لتحديد موقع النقطة ، باستخدام استبدال النقطة في متغيري x و y ثم مقارنة النتائج بمربع نصف قطر الدائرة.

النقطة M (x ₁ ، y ₁ ) تكمن:

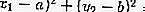
على الدائرة:

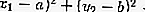
داخل الدائرة:

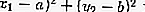
خارج الدائرة:

مع المركز O (0،0) ونصف القطر r

إذا كانت نقطة المركز عند O (0،0) ، فقم بالاستبدال في الجزء السابق ، أي:

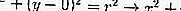
من المعادلة أعلاه ، يمكن تحديد موقع نقطة على الدائرة.

النقطة M (x ₁ ، y ₁ ) تكمن:

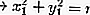
على الدائرة:

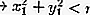
داخل الدائرة:

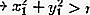
خارج الدائرة: اقرأ أيضًا: الفن هو: التعريف والوظيفة والأنواع والأمثلة [كامل]

يمكن التعبير عن الشكل العام للمعادلة في الأشكال التالية.

(س - أ) 2 + (ص - ب) 2 = r2 ، أو

X2 + y2 - 2ax - 2by + a2 + b2 - r2 = 0 ، أو

X2 + y2 + Px + Qy + S = 0 ، حيث P = -2a و Q = -2b و S = a2 + b2 - r2

تقاطع الخطوط والدوائر

يمكن تحديد دائرة بالمعادلة x2 + y2 + Ax + By + C = 0 ما إذا كان الخط h بالمعادلة y = mx + n لا يلمسها أو يسيء إليها أو يتقاطع معها باستخدام مبدأ التمييز.

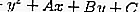
……. (المعادلة 1)

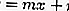
…… .. (المعادلة 2)

باستبدال المعادلة 2 في المعادلة 1 ، ستحصل على معادلة تربيعية ، وهي:

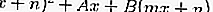
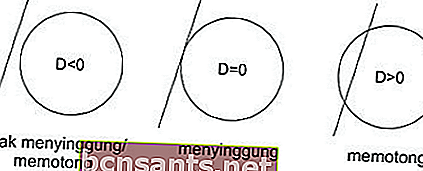
من المعادلة التربيعية أعلاه ، بمقارنة القيم المميزة ، يمكن ملاحظة ما إذا كان الخط لا يسيء / يقطع الدائرة أو يسيء إليها أو يتقاطع معها.

الخط h لا يتقاطع مع الدائرة ، لذا D <0

الخط h مماس للدائرة ، لذا D = 0

يتقاطع الخط h مع الدائرة ، لذا D> 0

معادلات المماسات إلى الدوائر

1. معادلة الظل عبر نقطة على دائرة

ماسات الدائرة تلتقي بالضبط بنقطة تقع على الدائرة. من نقطة تقاطع المماس والدائرة ، يمكن تحديد معادلة خط المماس.

يمكن تحديد معادلة مماس الدائرة عبر النقطة P (x ₁ ، y ₁ ) وهي:

• شكل

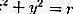
معادلة الظل

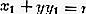
• شكل

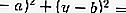
معادلة الظل

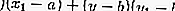
• شكل

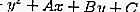
معادلة الظل

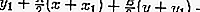
مثال على المشاكل:

معادلة المماس عبر النقطة (-1،1) في الدائرة

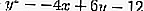
هي:

إجابة:

تعرف على معادلة الدائرة

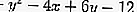
حيث أ = -4 ، ب = 6 ، ج = -12 ، س ₁ = -1 ، ص ₁ = 1

PGS هو

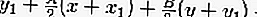
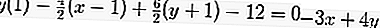
إذن ، معادلة المماس هي

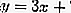
2. معادلة مماسات التدرج

إذا كان الخط الذي يحتوي على ميل m مماسًا لدائرة ،

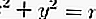
ثم معادلة الظل هي:

إذا كانت دائرة ،

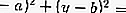
ثم معادلة الظل:

إذا كانت دائرة ،

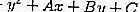
ثم معادلة الظل باستبدال r بـ ،

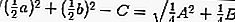
لهذا السبب:

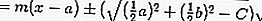
أو

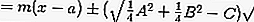
3. معادلات الظل للنقاط خارج الدائرة

من نقطة خارج الدائرة ، يمكن رسم مماسين للدائرة.

اقرأ أيضًا: الديمقراطية: التعريف والتاريخ والأنواع [كامل]

للعثور على معادلة الظل ، يتم استخدام صيغة معادلة الخط العادي ، وهي:

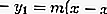
ومع ذلك ، من هذه الصيغة ، قيمة منحدر الخط غير معروفة. لإيجاد ميل الخط المستقيم ، عوض بمعادلة الدائرة. نظرًا لأن الخط ظل ، فمن المعادلة ينتج عن الاستبدال للقيمة D = 0 ، وسيتم الحصول على قيمة m

مثال على المشاكل

مثال مشكلة 1

الدائرة مركزها (2 ، 3) وقطرها 8 سم. معادلة الدائرة ...

نقاش:

لأن d = 8 تعني r = 8/2 = 4 ، لذا فإن معادلة الدائرة المكونة هي

(س - 2) ² + (ص - 3) ² = 42

x² - 4x + 4 + y² -6y + 9 = 16

x² + y² - 4x - 6y - 3 = 0

مثال مشكلة 2

أوجد المعادلة العامة للدائرة المتمركزة عند النقطة (5،1) والمخالفة للخط 3 س - 4 ص + 4 = 0!

نقاش:

إذا كان معروفًا أن مركز الدائرة ( أ ، ب ) = (5،1) وظل الدائرة هو 3 س - 4 ص + 4 = 0 ، فإن نصف قطر الدائرة تتم صياغته على النحو التالي.

وبالتالي ، فإن المعادلة العامة للدائرة هي كما يلي.

وبالتالي ، فإن المعادلة العامة لدائرة متمركزة عند (5،1) والمخالفة للخط 3 x - 4 y + 4 = 0 هي

مثال مشكلة 3

أوجد المعادلة العامة لدائرة مركزها (-3،4) وتخالف المحور ص!

نقاش:

بادئ ذي بدء ، لنرسم الرسم البياني للدائرة أولاً ، والذي يتمركز عند (-3،4) ويخالف المحور ص!

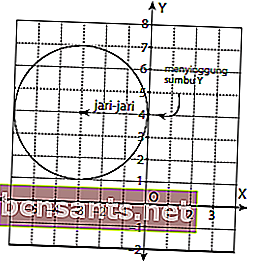
بناءً على الصورة أعلاه ، يمكن ملاحظة أن مركز الدائرة عند الإحداثيات (-3،4) بنصف قطر 3 ، بحيث:

وبالتالي ، فإن المعادلة العامة التي تتمحور حول (-3،4) والتي تسيء إلى المحور ص هي

في بعض الحالات ، يكون نصف قطر الدائرة غير معروف ، لكن الظل معروف. فكيف نحدد نصف قطر الدائرة؟ انظر إلى الصورة التالية.

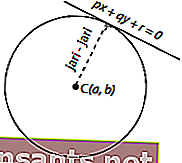
توضح الصورة أعلاه أن ظل المعادلة px + qy + r = 0 يتعلق بالدائرة المتمركزة في C ( a ، b ). يمكن تحديد نصف القطر بالمعادلة التالية. أ ، ب ). يمكن تحديد نصف القطر بالمعادلة التالية.

ربما يكون مفيدا.