
محيط المثلث هو الطول الكلي لضلع المثلث. إذن ، فإن صيغة محيط المثلث هي K = a + b + c أو مجموع كل جوانب المثلث.
عندما تدور حول الحديقة المثلثة ، ماذا يعني ذلك؟ نعم! أنت تدور حول شكل مثلث. ما هو شكل المثلث المسطح؟ فيما يلي شرح للمثلث ، ونوع المثلث ، وكيفية تحديد أو معادلة محيط المثلث.
شرح المثلث
المثلث هو شكل يتكون من ثلاثة خطوط متقاطعة تشكل زاوية. عدد زوايا المثلث يساوي 180 درجة.
المثلثات هي أبسط الأشكال المسطحة لأنها عناصر تشكل أشكالًا مسطحة أخرى مثل المربعات والمستطيلات والدوائر وعناصر الأشكال المسطحة التي تشكل أشكالًا مثل المنشورات والأهرامات.
خصائص المثلث
لمزيد من شرح معنى المثلث ، سأرسم شكل مثلث عشوائي ABC أدناه:
تتضمن العناصر الموجودة في مثلث ABC ما يلي:
- تُعرف النقاط A و B و C بالرؤوس.
- تسمى الخطوط AB و BC و CA أضلاع المثلث.
- يمكن رؤية المثلثات المختلفة من أطوال الأضلاع والزوايا التي شكلها المثلث.
أنواع المثلثات
تختلف أنواع المثلثات بشكل كبير بناءً على طول الأضلاع والزوايا التي تشكل المثلث. فيما يلي تقسيم أنواع المثلثات
أنواع المثلثات على أساس أطوال الأضلاع
- مثلث متساوي الاضلاع
وهو مثلث له الأضلاع الثلاثة بنفس الطول. بالإضافة إلى ذلك ، فإن الزوايا الثلاث المكونة من المثلث الضلع لها نفس الحجم ، وهو 60 درجة ، لأن عدد زوايا المثلث يساوي 180 درجة.
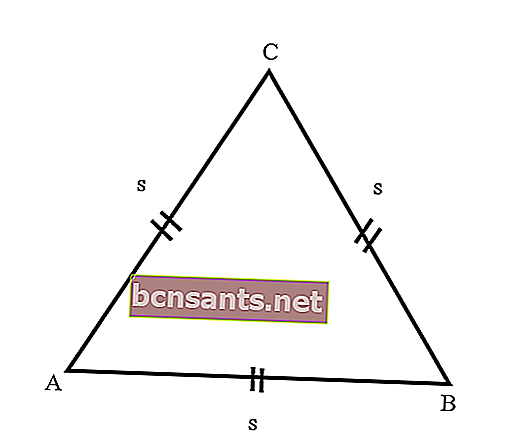
لمعرفة المزيد عن المثلثات متساوية الأضلاع ، ضع في اعتبارك الشرح التالي لخصائص المثلثات متساوية الأضلاع:

في الشكل (ب) - (د) ، يبدو أن شكل المثلث ABC يمكن أن يشغل إطاره تمامًا باستخدام 3 طرق ، أي التدوير بقدر 120 درجة متمركزة على النقطة O (انظر إلى اتجاه الدوران) على (الشكل ب) استدارة بقدر 240 درجة في مركز الدوران في O (في الشكل ج) والتي تدور 360 درجة (دورة كاملة واحدة) عند نقطة المركز عند O (في الشكل د)
اقرأ أيضًا: صيغ الفرص وأمثلة على المشكلاتوفقًا لشرح الأشكال من أ إلى و ، فإن المثلث المتساوي الأضلاع ABC له تناظر دوراني يصل إلى المستوى 3. وفي الوقت نفسه ، يمكن للأشكال e و f و g التي تم عكسها أن تشغل الإطار بشكل صحيح. لهذا ، يحتوي شكل المثلث ABC على 3 محاور للتماثل. بينما في الصورة أعلاه ، محاور التناظر هي CD و BF و AE. بحيث يمكن للمثلث متساوي الأضلاع أن يشغل الإطار 6 طرق بالضبط.
بناءً على بعض الأوصاف أعلاه ، تتضمن بعض الخصائص الموجودة في مثلث متساوي الأضلاع: يحتوي على 3 مستويات من التناظر الدوراني ، و 3 محاور تناظر ، و 3 جوانب متساوية الأضلاع ، و 3 زوايا متساوية 60 درجة ، ويمكن أن يشغل الإطار حتى 6 طرق.
- مثلث متساوي الساقين
وهو مثلث له ضلع واحد بنفس الطول. يحتوي المثلث المتساوي الساقين على زاويتين متساويتين ، أي الزاويتان متقابلتان.
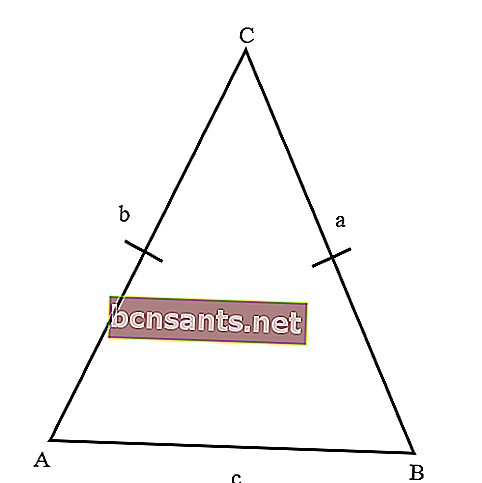
فيما يلي خصائص مثلث متساوي الساقين ؛
- بناء مثلث متساوي الساقين ، مع تدويره لدورة كاملة واحدة ، يشغل الإطار تمامًا بطريقة واحدة. بحيث يكون لمثلث samakaki تناظر دوار يساوي واحدًا.
- في الوقت نفسه ، يحتوي المثلث متساوي الساقين على محور تناظر واحد فقط.
- أي مثلث
أي مثلث بثلاثة أضلاع ليست بنفس الطول والزوايا الثلاث غير متساوية.

فيما يلي خصائص أي مثلث:
- له ثلاثة جوانب ليست بنفس الطول. (في الصورة أعلاه ، فإن الجوانب الثلاثة المقصودة هي طول BA CB ≠ AC).
- ليس لديه تناظر أضعاف.
- له تناظر دوار واحد فقط.
- الزوايا الثلاث لها أحجام مختلفة.
أنواع المثلثات على أساس الزاوية
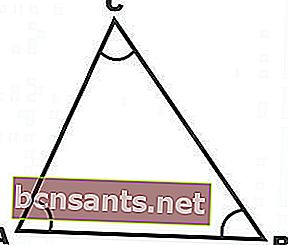
- مثلث حاد الزوايا
أي مثلث به زواياه الثلاث يشكل زاوية حادة. الزاوية الحادة هي الزاوية التي تتراوح من 0 إلى 90 درجة.
- مثلث بلانت
وهو مثلث بزاوية واحدة تشكل زاوية منفرجة. الزاوية المنفرجة هي الزاوية التي يتراوح حجمها بين 90 و 180 درجة.
اقرأ أيضًا: حلول للصيغ التي غالبًا ما تُنسى!
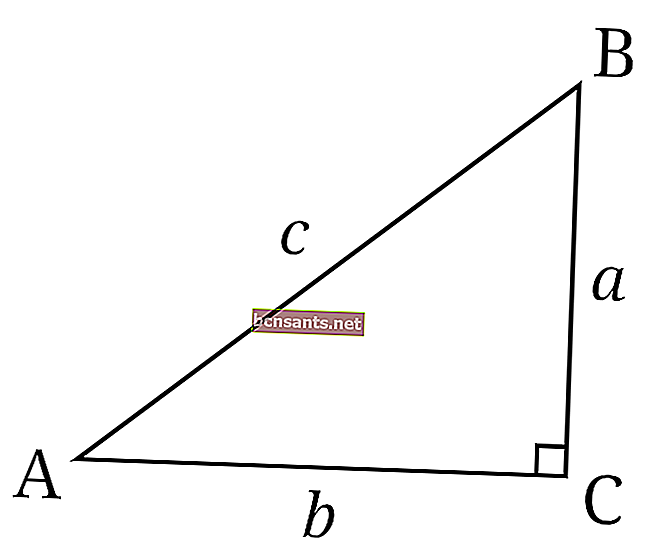
- مثلث قائم
وهو مثلث بزاوية إحدى أركانه 90 درجة.
صيغة محيط المثلث
يتم الحصول على محيط الشكل من عدد أطوال الحواف (sisis) التي تشكل الشكل.
إذن ، يمكن الحصول على صيغة محيط المثلث بجمع كل ضلع من أضلاع المثلث.
محيط المثلث = طول الضلع الأول + طول الضلع الثاني + طول الضلع الثالث
ك = أ + ب + ج
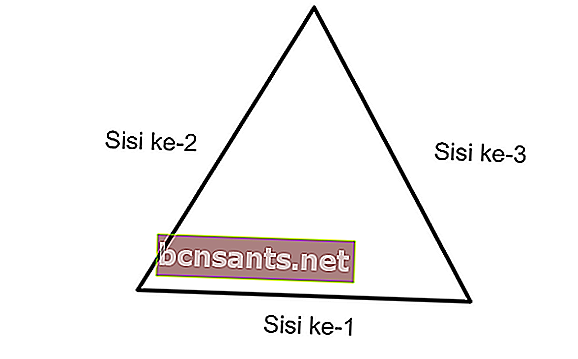
مثال مشكلة إيجاد محيط المثلث
مثال مشكلة 1.
مثلث متساوي الأضلاع طول ضلعه 3 سم فما محيطه!
المحلول:
أنت تعرف: ق = 3 سم
مطلوب: محيط المثلث؟
إجابة:
المثلثات متساوية الأضلاع لها نفس الجوانب ،
ك = ث + ث + ث
ك = 3 + 3 + 3
K = 9 سم
إذن ، محيط المثلث متساوي الأضلاع يساوي 9 سم.
مثال مشكلة 2.
يبلغ إجمالي طول ضلع مثلث متساوي الساقين 36 cm. أطول طول ضلع 13 سم. ما هو طول اقصر ضلع؟
المحلول:
أنت تعلم أن = K = 36 سم ؛ ب = أ = 13 سم
مطلوب : أقصر طول ضلع؟
الجواب :
محيط المثلث = أ + ب + ج
36 = 13 + 13 + ج
ج = 10 سم
إذن ، أقصر طول ضلع في المثلث هو 10 سم
مثال مشكلة 3.
تحصل على أي مثلث أضلاعه 9 ، 11 ، 13 سم لكل منهما. احسب محيط المثلث!
المحلول:
من المعروف أن : أ = 13 سم ؛ ب = 9 سم ؛ ج = 11 سم
مطلوب : محيط المثلث؟
إجابة:
ك = أ + ب + ج
ك = 13 +9 +11
K = 33 سم
إذن ، محيط المثلث يساوي 33 سم
مشكلة المثال 4.
احسب محيط المثلث متساوي الساقين بمساحة 12 cm2 وطول ضلعه 6 cm!
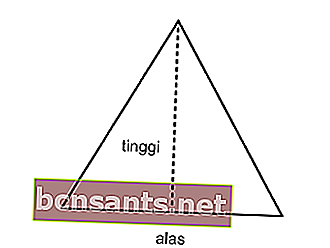
المحلول:
أنت تعرف: L = 12 سم 2 ؛ أ = 6 سم
مطلوب: محيط المثلث؟
إجابة:
لإيجاد محيط المثلث ، يجب أن تعرف طول أضلاع المثلث.
استخدم المساحة لإيجاد ارتفاع المثلث
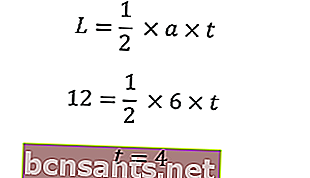
باستخدام نظام فيثاغورس ، نعرف وتر المثلث متساوي الساقين عن طريق إدخال طول القاعدة (أ) وارتفاع المثلث (تي)

باستخدام المعادلة أعلاه ، نحصل على وتر المثلث
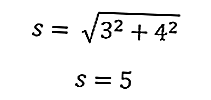
سيسمح لك ذلك بحساب محيط المثلث على الفور
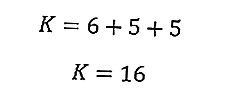
إذن ، محيط المثلث يساوي 16 سم
المرجع : المثلث - الرياضيات ممتعة
