
معادلة الانحراف المعياري أو ما يسمى الانحراف المعياري هي تقنية إحصائية تستخدم لشرح تجانس المجموعة.
يمكن أيضًا استخدام الانحراف المعياري لشرح كيفية توزيع البيانات في عينة ، بالإضافة إلى العلاقة بين النقاط الفردية والمتوسط أو القيمة المتوسطة للعينة.
قبل أن نناقش أكثر ، هناك بعض الأشياء التي نحتاج إلى معرفتها أولاً ، وهي أين:
يمكن أن يكون الانحراف المعياري لمجموعة البيانات صفرًا أو أكبر أو أقل من الصفر.
هذه القيم المتغيرة لها المعاني التالية:
- إذا كان الانحراف المعياري صفراً ، فإن جميع قيم العينة في مجموعة البيانات متساوية.
- وفي الوقت نفسه ، تشير قيمة الانحراف المعياري الأكبر أو الأقل من الصفر إلى أن نقطة بيانات الفرد بعيدة عن متوسط القيمة.

خطوات إيجاد الانحراف المعياري
لتحديد قيمة الانحراف المعياري والعثور عليها ، نحتاج إلى اتباع الخطوات أدناه.
- الخطوة الأولى
احسب متوسط أو متوسط القيمة عند كل نقطة بيانات.
يمكنك القيام بذلك عن طريق إضافة كل قيمة في مجموعة البيانات ثم يتم تقسيم الرقم على إجمالي عدد النقاط من البيانات.
- الخطوة التالية
احسب تباين البيانات عن طريق حساب الانحراف أو الاختلاف لكل نقطة بيانات من متوسط القيمة.
ثم يتم تربيع قيمة الانحراف عند كل نقطة بيانات وإزالتها بمربع القيمة المتوسطة.
بعد الحصول على قيمة التباين ، يمكننا حساب الانحراف المعياري عن طريق تأصيل قيمة التباين.
اقرأ أيضًا: السرد: التعريف والغرض والخصائص والأنواع والأمثلةصيغ الانحراف المعياري
1. الانحراف المعياري للسكان
يتم ترميز السكان بواسطة σ (سيغما) ويمكن تعريفه بالصيغة:

2. عينة الانحراف المعياري
الصيغة هي:
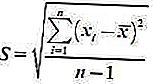
3. معادلة الانحراف المعياري للعديد من مجموعات البيانات
لمعرفة توزيع البيانات من عينة ، يمكننا تقليل كل قيمة بيانات بمتوسط القيمة ، ثم تتم إضافة جميع النتائج.
ومع ذلك ، إذا استخدمت الطريقة أعلاه ، فستكون النتيجة دائمًا صفرًا ، لذلك لا يمكن استخدام هذه الطريقة.

حتى لا تكون النتيجة صفرًا (0) ، يجب علينا أولاً ضبط التخفيض في قيمة البيانات ومتوسط القيمة ، ثم جمع جميع النتائج.
باستخدام هذه الطريقة ، سيكون لنتيجة مجموع المربعات قيمة موجبة.

سيتم الحصول على قيمة التباين بقسمة مجموع المربعات على عدد أحجام البيانات (ن).
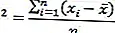
ومع ذلك ، إذا استخدمنا هذه القيمة المتغيرة للعثور على تباين المحتوى ، فستكون قيمة التباين أكبر من متغير العينة.
للتغلب على هذا ، يجب استبدال حجم البيانات (n) كمقسم بدرجات الحرية (n-1) بحيث تقترب قيمة تباين العينة من متغير المحتوى.
وبالتالي يمكن كتابة صيغة نموذج العينة على النحو التالي:

قيمة المتغير التي تم الحصول عليها هي القيمة التربيعية ، لذلك نحتاج إلى تربيعها أولاً للحصول على الانحراف المعياري.

لتسهيل الحساب ، يمكن اختزال صيغة التباين والانحراف المعياري إلى الصيغة أدناه.
صيغ متغيرات البيانات
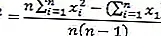
صيغة الانحراف المعياري
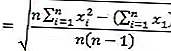
ملاحظات :
s2 = متغير
s = الانحراف المعياري
x i = قيمة ith x
ن = حجم العينة
مثال على مشاكل الانحراف المعياري
ما يلي هو مثال والعمل على مشاكل الانحراف المعياري.
سؤال:
تتولى ساندي ، كرئيسة للأعضاء اللامنهجيين ، مهمة تسجيل الارتفاع الإجمالي للأعضاء. البيانات التي جمعتها كلمة المرور هي كما يلي:
167 ، 172 ، 170 ، 180 ، 160 ، 169 ، 170 ، 173 ، 165 ، 175
من البيانات أعلاه ، احسب الانحراف المعياري!
اقرأ أيضًا: شفرة مورس: التاريخ والصيغ وطرق الحفظالجواب :
| أنا | س ط | س ط 2 |
| 1 | 167 | 27889 |
| 2 | 172 | 29584 |
| 3 | 170 | 28900 |
| 4 | 180 | 32400 |
| 5 | 160 | 25600 |
| 6 | 169 | 28561 |
| 7 | 170 | 28900 |
| 8 | 173 | 29929 |
| 9 | 165 | 27225 |
| 10 | 175 | 30625 |
| Σ | 1710 | 289613 |
من البيانات أعلاه ، يمكن ملاحظة أن عدد البيانات (ن) = 10 ودرجات الحرية (ن -1) = 9 أيضًا
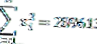
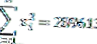
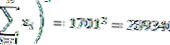
حتى نتمكن من حساب قيمة التباين كالتالي:

القيمة المتغيرة لبيانات Sandi التي تم جمعها هي 30.32 . لحساب الانحراف المعياري ، نحتاج فقط إلى ضبط قيمة التباين بحيث:
ق = -30.32 = 5.51
إذن ، الانحراف المعياري للمشكلة أعلاه هو 5.51
الفوائد والتطبيقات
يستخدم الإحصائيون الانحراف المعياري بشكل شائع لتحديد ما إذا كانت البيانات المأخوذة تمثل المجتمع بأكمله.

على سبيل المثال ، يريد شخص ما معرفة وزن طفل صغير يتراوح عمره بين 3 و 4 سنوات في القرية.
لتسهيل الأمر ، نحتاج فقط إلى معرفة وزن عدد قليل من الأطفال ثم حساب المتوسط والانحراف المعياري.
من قيم الانحراف المعياري والمتوسط ، يمكننا تمثيل وزن الجسم الكامل للأطفال الذين تتراوح أعمارهم بين 3-4 سنوات في القرية.
مرجع
- الانحراف المعياري - صيغ لكيفية البحث عن المشاكل وأمثلة عليها
- الانحراف المعياري: معادلات الحساب وأمثلة على المشكلات
