
وظيفة التركيب هي مزيج من عملية لنوعين من الوظائف f (x) و g (x) بحيث يمكن أن تنتج وظيفة جديدة.
صيغ وظيفة التركيب
رمز عملية وظيفة التكوين هو مع "o" ثم يمكن قراءة التكوين أو الدائرة. يمكن تشكيل هذه الوظيفة الجديدة من f (x) و g (x) ، وهي:
- (fog) (x) مما يعني أن g تم إدخالها في f
- (gof) (x) مما يعني وضع f في g
تُعرف وظيفة التكوين أيضًا باسم وظيفة واحدة.
ما هي وظيفة واحدة؟
الوظيفة الواحدة هي وظيفة يمكن الإشارة إليها بالحروف "fog" أو يمكن قراءتها "f roundabout g". وظيفة "الضباب" هي وظيفة g التي تتم أولاً ثم تليها f.
وفي الوقت نفسه ، تقرأ وظيفة "gof" الدالة g دوار f. وبالتالي ، فإن "gof" هي وظيفة حيث يتم عمل f أولاً بدلاً من g.
ثم الوظيفة (fog) (x) = f (g (x)) → الوظيفة g (x) تتكون كدالة f (x)
لفهم هذه الوظيفة ، ضع في اعتبارك الصورة أدناه:
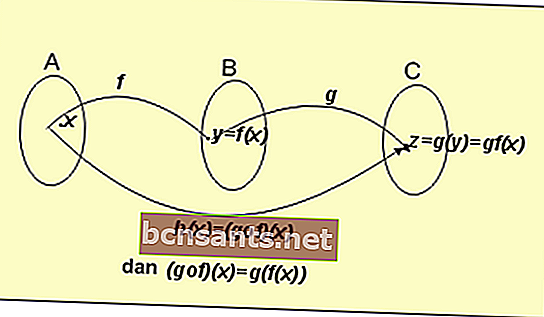
من مخطط الصيغة أعلاه ، التعريف الذي حصلنا عليه هو:
إذا تم تحديد f: A → B بواسطة الصيغة y = f (x)
إذا تم تحديد g: B → C بواسطة الصيغة y = g (x)
ثم نحصل على نتيجة الوظيفتين g و f:
ح (س) = (جوف) (س) = ز (و (س))
من التعريف أعلاه يمكننا أن نستنتج أنه يمكن كتابة الوظائف التي تتضمن الدالتين f و g:
- (gof) (x) = g (f (x))
- (ضباب) (x) = f (g (x))
خصائص وظيفة التركيب
هناك عدة خصائص لوظيفة التركيب موضحة أدناه.
إذا كانت f: A → B ، g: B → C ، h: C → D ، إذن:
- (ضباب) (x) ≠ (gof) (x). لا تنطبق الطبيعة التبادلية
- [fo (goh) (x)] = [(fog) oh (x)]. ترابطية
- إذا كانت وظيفة الهوية هي I (x) ، إذن (fol) (x) = (lof) (x) = f (x)
مثال على المشاكل
المشكلة 1
إعطاء وظيفتين ، كل من f (x) و g (x) ، على التوالي ، وهما:
و (س) = 3 س + 2
ز (س) = 2 - س
تحديد:
أ) ( و س ز ) (س)
ب) ( ز س و ) (س)
إجابة
معروف:
و (س) = 3 س + 2
ز (س) = 2 - س
( f o g ) (x)
"أدخل g (x) في f (x)"
أن تكون:
( f o g ) (x) = f ( g (x))
= و (2 - س)
= 3 (2 - س) + 2
= 6 - 3 س + 2
= - 3 س + 8
( ز س و ) (س)
"أدخل f (x) في g (x)"
حتى تصبح:
( f o g ) (x) = g ( f (x))
= ز (3 س + 2)
= 2 - (3 س + 2)
= 2 - 3 س - 2
= - 3x
المشكلة 2
إذا كان معروفًا أن f (x) = 3x + 4 و g (x) = 3x فما قيمة (fog) (2).
إجابة:
(ضباب) (x) = f (g (x))
= 3 (3 س) + 4
= 9 س + 4
(ضباب) (2) = 9 (2) + 4
= 22
مشكلة 3
بالنظر إلى الدالة f (x) = 3x - 1 و g (x) = 2 × 2 + 3. قيمة تكوين الدالة ( g o f ) (1) =….؟
إجابة
معروف:
f (x) = 3x - 1 و g (x) = 2 × 2 + 3
( ز س و ) (1) = ...؟
أدخل f (x) في g (x) ثم املأ بالرقم 1
( ز س و ) (س) = 2 (3 × - 1) 2 + 3
( ز س و ) (س) = 2 (9 × 2 - 6X + 1) + 3
( ز س و ) (س) = 18X 2 - 12X + 2 + 3
( ز س و ) (س) = 18 × 2 - 12X + 5
( ز س و ) (1) = 18 (1) 2-12 (1) + 5 = 11
المشكلة 4
يتم إعطاء وظيفتين:
و (س) = 2 س - 3
ز (س) = س 2 + 2 س + 3
إذا كانت (fog) (a) تساوي 33 ، فأوجد قيمة 5a
إجابة:
البحث أولاً (ضباب) (x)
(ضباب) (x) يساوي 2 (x2 + 2x + 3) - 3
(ضباب) (x) يساوي 2 × 2 4x + 6 - 3
(fog) (x) يساوي 2 × 2 4x + 3
33 هو نفس 2a2 4a + 3
2a2 4a - 30 يساوي 0
a2 + 2a - 15 يساوي 0
اقرأ أيضًا: معادلات الأعمال: شرح للمادة ، أمثلة على الأسئلة والمناقشةعامل:
(أ + 5) (أ - 3) يساوي 0
أ = - 5 أو يساوي 3
إلى
5a = 5 (−5) = 25 أو 5a = 5 (3) = 15
المشكلة 5
إذا كانت (fog) (x) = x² + 3x + 4 and g (x) = 4x - 5. ما قيمة f (3)؟
إجابة:
(ضباب) (x) يساوي x² + 3x + 4
f (g (x)) تساوي x² + 3x + 4
g (x) تساوي 3 لذا ،
4x - 5 يساوي 3
4x يساوي 8
س يساوي 2
f (g (x)) = x² + 3x + 4 وبالنسبة إلى g (x) تساوي 3 نحصل على x يساوي 2
حتى: f (3) = 2² + 3. 2 + 4 = 4 + 6 + 4 = 14
وبالتالي فإن التفسير المتعلق بصيغة وظيفة التركيب هو مثال على المشكلة. ربما يكون مفيدا.
