
بناء الفضاء هو موضوع تتم مناقشته غالبًا في الرياضيات ، وغالبًا ما تكون الصيغة مشكلة رياضية في المرحلتين الابتدائية والإعدادية.
يمكن تفسير مساحة المبنى على أنها مبنى يحتوي على حجم أو محتوى رياضيًا. يمكن أيضًا تفسير أن شكل الفضاء هو شكل ثلاثي الأبعاد له حجم أو مساحة ومحدودة بجوانب.
هناك أشكال مختلفة من الفضاء نفسه ، مثل الكتل والمكعبات والأنابيب والكرات وما إلى ذلك.
كل من هذه الأشكال له معادلة للحجم ومساحة السطح على التوالي. هذا يجعل أحيانًا من الصعب على العديد من الطلاب تذكرها.
لقد قمت هنا بإعداد قائمة كاملة بصيغ البناء ، بحيث يمكنك بسهولة حل العديد من مسائل الرياضيات في هذا الموضوع.
1. مكعب
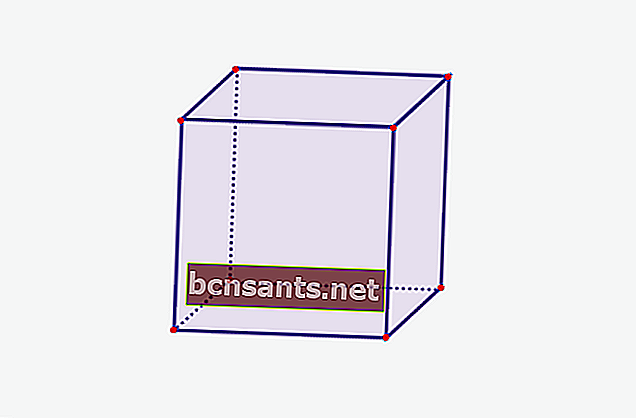
| حجم المكعب | V = sxsxs |
| مساحة سطح المكعب | L = 6 س (س س) |
| ضع دائرة حول المكعب | ك = 12 س |
| منطقة جانب واحد | L = sxs |
2. الحزم
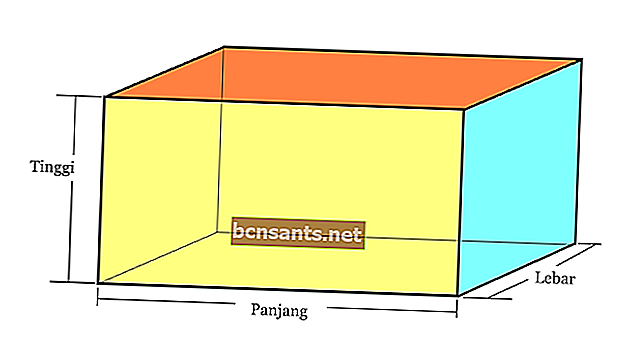
| حجم الكتلة | V = pxlxt |
| مساحة سطح الكتلة | L = 2 x (pl + lt + pt) |
| مساحة قطرية | د = √ ( p2 + l2 + t2) |
| محيط الشعاع | ك = 4 س (ث + ل + ح) |
3. المنشور الثلاثي
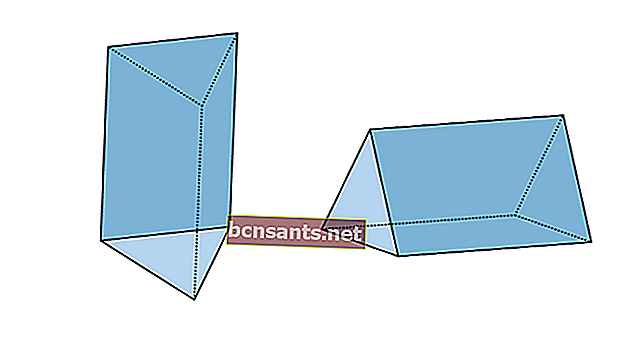
| حجم المنشور الثلاثي | V = مساحة القاعدة xt |
| مساحة سطح المنشور الثلاثي | L = محيط القاعدة xt + 2 x مساحة قاعدة المثلث |
4. الخامس الرباعي
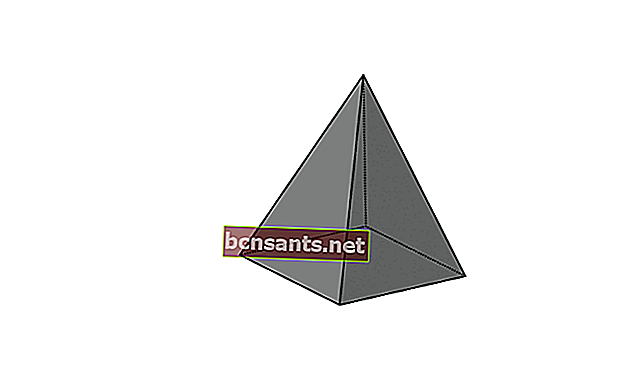
| حجم الهرم | الخامس = 1/3 xpxlxt |
| مساحة سطح الهرم | L = مساحة القاعدة + مساحة غلاف الهرم |
5. المثلث الخامس
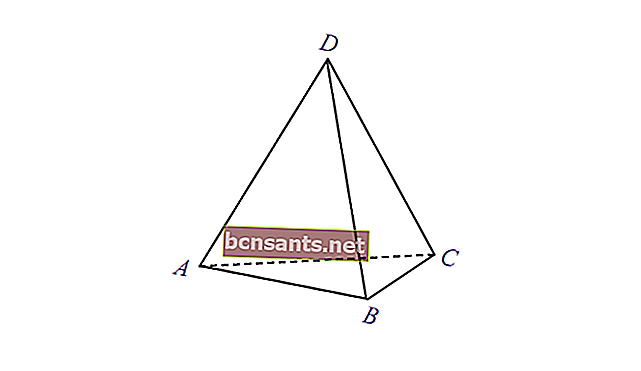
| حجم الهرم | V = 1/3 x مساحة القاعدة xt |
| مساحة السطح | L = مساحة القاعدة + مساحة غلاف الهرم |
6. الأنابيب

| حجم الأنبوب | V = π x r2 xt |
| مساحة سطح الأنبوب | L = (2 × مساحة القاعدة) + (محيط القاعدة × الارتفاع) |
7. المخاريط

| حجم المخروط | V = 1/3 x π x r2 xt |
| مساحة سطح المخروط | أ = (π س ر 2) + (π س س س) |
8 الكرة

| حجم الكرة | V = 4/3 x π x r3 |
| مساحة سطح الكرة | أ = 4 س π س ر 2 |
جدول كامل لصيغ البناء
يمكنك أيضًا الحصول على القائمة أعلاه باختصار من خلال النظر إلى الجدول أدناه. يمكنك أيضًا حفظ هذه الصورة حتى تتمكن من رؤيتها مرة أخرى في أي وقت.
هذا شرح لصيغة نموذج المبنى لحساب الحجم ومساحة السطح.
نأمل أن يساعدك الشرح أعلاه في فهم شكل الفضاء ، بحيث يمكنك استخدامه لحل مسائل الرياضيات وتطبيقاتها المختلفة في الحياة اليومية.
مرجع
- مراجعة صيغ الحجم - Khan Academy
- ورقة الصيغة الهندسية
