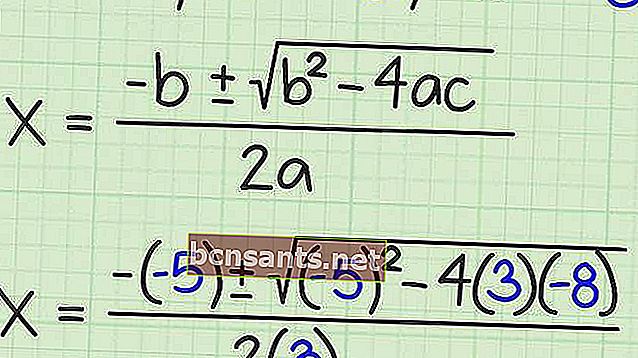
صيغة ABC هي طريقة ممتازة لإيجاد جذور الأشكال المختلفة من المعادلات التربيعية حتى لو لم تكن النتيجة عددًا صحيحًا.
يمكن حل المعادلة التربيعية ax2 + bx + c = 0 باستخدام عدة طرق. من بينها طريقة التحليل واستكمال المربع ABC والصيغة.
من بين هذه الطرق ، تعتبر صيغة abc واحدة ممتازة لأنه يمكن استخدامها للعثور على جذور الأشكال المختلفة من المعادلات التربيعية حتى لو لم تكن النتيجة عددًا صحيحًا.
فيما يلي شرح إضافي للصيغة ، بما في ذلك الفهم والأسئلة والمناقشة.
فهم صيغة ABC
صيغة abc هي إحدى الصيغ المستخدمة لإيجاد جذور المعادلة التربيعية. هنا شكل عام لهذه الصيغة.

تسمى الأحرف a و b و c في الصيغة abc المعاملات. معامل تربيع x2 هو a ، ومعامل x هو b ، و c هو معامل الثابت ، ويشار إليه عادةً بمصطلح ثابت أو مستقل.
المعادلة التربيعية هي في الأساس معادلة رياضية تشكل الهندسة المنحنية للقطع المكافئ في الربع xy.
قيمة المعامل في الصيغة abc لها عدة معانٍ على النحو التالي:
- يحدد a المقعر / المحدب prabola التي تشكلها المعادلة التربيعية. إذا كانت القيمة> 0 ، فسيتم فتح القطع المكافئ لأعلى. ومع ذلك ، إذا كانت القيمة <0 ، فإن القطع المكافئ سيفتح لأسفل.
- يحدد b الموضع x للذروة المكافئة ، أو القيمة المتماثلة المرآة للمنحنى. الموضع الدقيق لمحور التناظر هو -b / 2a للمعادلة التربيعية.
- يحدد c نقطة تقاطع دالة المعادلة التربيعية المكافئة المتكونة على المحور y أو عندما تكون قيمة x = 0.
أمثلة على الأسئلة والمناقشة
فيما يلي بعض الأمثلة على مشاكل المعادلات التربيعية ومناقشتها مع الحلول باستخدام صيغ المعادلات التربيعية.
1. حل جذور المعادلة التربيعية x2 + 7x + 10 = 0 باستخدام الصيغة abc!
إجابة:
اقرأ أيضًا: 7 وظائف بروتينية للجسم [شرح كامل]لاحظ أن أ = 1 ، ب = 7 ، ج = 10
إذن ، جذور المعادلة هي:

إذن ، حاصل ضرب جذور المعادلة x2 + 7x + 10 = 0 هو x = -2 أو x = -5
2. باستخدام الصيغة abc ، أوجد مجموعة الحلول لـ x2 + 2x = 0
إجابة:
بالنظر إلى أن أ = 1 ، ب = 1 ، ج = 0
ثم تكون جذور المعادلة كما يلي:

وبالتالي ، فإن حاصل ضرب جذور المعادلة x2 + 2x = 0 هو x1 = 0 و x2 = -2 ، وبالتالي فإن مجموعة الحلول هي HP = {-2،0}
3. أوجد مجموعة الجذور x في المسألة x2 - 2x - 3 = 0 باستخدام الصيغة abc
إجابة:
بالنظر إلى أن أ = 1 ، ب = 2 ، ج = -3
ثم تكون نتائج جذور المعادلة كما يلي:

وبالتالي ، مع x1 = -1 و x2 = -3 ، فإن مجموعة الحلول هي HP = {-1،3}
4. حدد نتيجة المعادلة التربيعية x 2 + 12x + 32 = 0 باستخدام الصيغة abc !
إجابة:
لاحظ أن أ = 1 ، ب = 12 ، ج = 32
ثم تكون جذور المعادلة كما يلي:

إذن ، نتائج الجذور للمعادلة التربيعية هي -4 و -8
5. أوجد المجموعة من المسألة التالية 3x2 - x - 2 = 0
إجابة:
لاحظ أن أ = 3 ، ب = -1 ، ج = -2
ثم تكون جذور المعادلة كما يلي:

وبالتالي ، فإن جذور المعادلة التربيعية 3x2 - x - 2 = 0 هي x1 = 1 ، و x2 = -2 / 3 ، لذا فإن مجموعة الحلول هي HP = {1، -2 / 3}
6. أوجد جذور المعادلة x 2 + 8x + 12 = 0 باستخدام الصيغة abc!
إجابة:
لاحظ أن أ = 1 ، ب = 8 ، ج = 12
ثم تكون جذور المعادلة التربيعية كما يلي:

إذن ، جذور المعادلة التربيعية x2 + 8x + 12 = 0 هي x1 = -6 أو x2 = -2 بحيث تكون مجموعة الحلول هي HP = {-6، -2}
7. حل جذور المعادلة x 2 - 6x - 7 = 0 بالصيغة abc .
إجابة:
نعلم أن أ = 1 ، ب = - 6 ، ج = - 7
ثم تكون جذور المعادلة كما يلي:
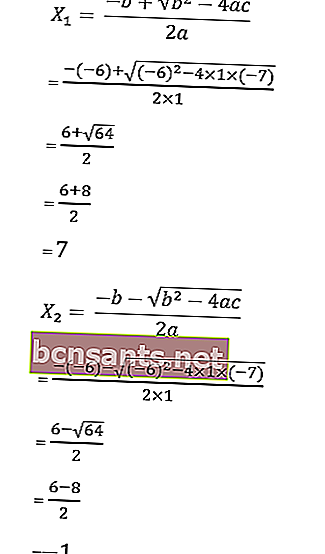
إذن ، الجذور هي x 1 = 1 أو x 2 = 5/2 ، لذا فإن مجموعة الحلول هي HP = {1، 5/2}.
اقرأ أيضًا: المعادلات التربيعية (FULL): التعريف ، الصيغ ، أمثلة على المشكلات8. أوجد جذور المعادلة 2x 2 - 7x + 5 = 0 بالصيغة abc
إجابة:
نعلم أن أ = 2 ، ب = - 7 ، ج = 5
ثم تكون جذور المعادلة كما يلي:
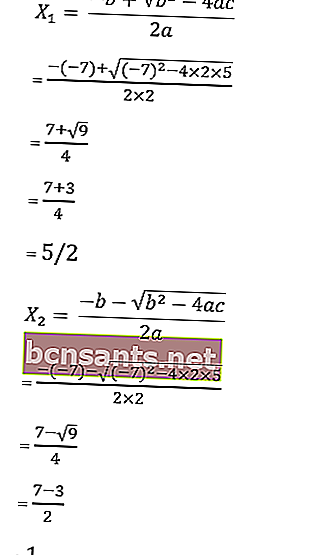
إذن ، الجذور هي x1 = –4 أو x2 = 5/3 بحيث تكون مجموعة الحلول HP = {1، 5/3}.
9. حل المعادلة 3x 2 + 7x - 20 = 0 بالصيغة abc.
إجابة:
لاحظ أن أ = 3 ، ب = 7 ، ج = - 20
ثم جذور المعادلة هي:
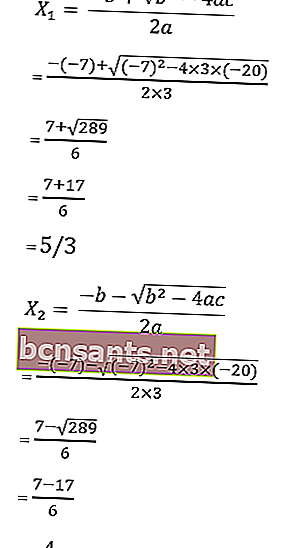
إذن ، الجذور هي x1 = –4 أو x2 = 5/3 ، لذا فإن مجموعة الحلول هي HP = {-4، 5/3}.
10. أوجد جذور المعادلة 2x 2 + 3x +5 = 0 بالصيغة abc.
إجابة:
معروف أن أ = 2 ، ب = 3 ، ج = 5
ثم تكون جذور المعادلة كما يلي:
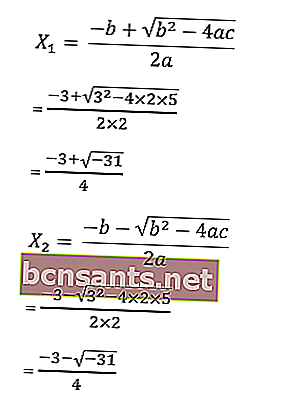
نتيجة جذر المعادلة 2x2 + 3x +5 = 0 لها العدد الجذر التخيلي √ - 31 ، لذلك ليس للمعادلة حل تمت كتابة مجموعة الحلول كمجموعة فارغة HP = {∅}
هذا شرح لتعريف صيغة abc مع أمثلة على الأسئلة ومناقشتها. ربما يكون مفيدا!
