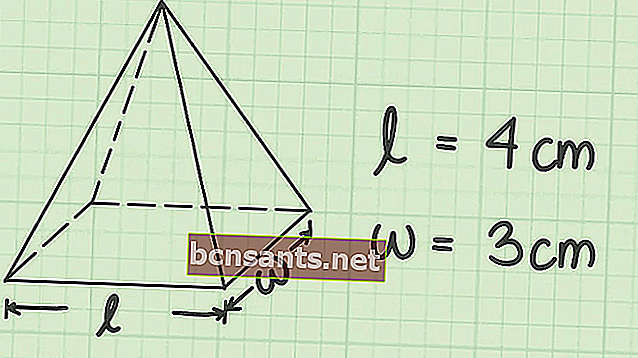
حجم الهرم = 1/3 × مساحة القاعدة × الارتفاع . في هذه الحالة ، تعتمد صيغة مساحة قاعدة الهرم على شكل الشكل الذي يتكون منه. تمت مناقشة هذه المقالة بالكامل.
ليماس عبارة عن مبنى له قاعدة متعددة الأطراف ذات جوانب عمودية مثلثة مع قمة في الأعلى.
مساحة البناء لها خصائصها الخاصة وكذلك الهرم. فيما يلي خصائص غرفة الهرم.
- المستوى العلوي للهرم نقطة حادة
- المستوى السفلي للهرم شكل
- المستوى الجانبي للهرم مثلث
عناصر ليماس
على غرار الهياكل الأخرى ، يتكون الهرم من عناصر تشمل:
- نقطة الزاوية
- الجانبي
- طائرة جانبية
نظرًا لأن الهرم يتكون من أشكال مختلفة من الفضاء ، فإن كل شكل له عدد من العناصر التي تختلف وفقًا لشكل شكل الهرم.
أنواع ليماس
لدى ليماس عدة أشكال من الفضاء بناءً على شكل القاعدة.
1. المثلث الخامس
وهو نوع من الهرم قاعدته مثلث متساوي الأضلاع أو متساوي الساقين أو أي مثلث.
عنصر الهرم الثلاثي:
- 4 نقاط ركنية
- 4 طائرات جانبية
- 6 ضلوع

2. المربعات الخامسة
هو نوع من الهرم قاعدته مستطيل (مربع ، مستطيل ، طائرة ورقية ، معين ، متوازي الأضلاع ، شبه منحرف ، وأشكال أخرى مستطيلة).
عنصر الهرم المستطيل:
- 5 نقاط ركنية
- 5 طائرات جانبية
- 8 ضلوع

3. خمس نقاط لياس
إنه نوع من الهرم له قاعدة خماسية مسطحة ، سواء كان خماسيًا منتظمًا أو أي خماسي.
عناصر الهرم الخماسي:
- 6 نقاط ركنية
- 6 طائرات جانبية
- 10 ضلوع

4. السداسي الخامس
إنه نوع من الهرم له شكل قاعدة سداسية الشكل ، سواء السداسية العادية أو السداسية التعسفية.
عنصر الهرم السداسي:
- 7 نقاط ركنية
- 7 طائرات جانبية
- 12 ضلع

تركيبة منطقة سطح ليماس
مساحة السطح هي المساحة الإجمالية للشكل الذي يشكل شكلاً. يتكون الشكل الذي يشكل الهرم من جوانب القاعدة ، وجوانب الجوانب المثلثة. لذلك ، بشكل عام ، تكون صيغة مساحة سطح الهرم كما يلي.
اقرأ أيضًا: تشريح الإنسان ووظائفه + صور [كاملة]صيغة مساحة سطح الهرم = مساحة القاعدة + مساحة جميع الجوانب المتعامدة
من أجل فهم أفضل لمفهوم مساحة سطح الهرم ، إليك مثال لمشكلة تتعلق بمساحة سطح الهرم.
مثال مشكلة 1.
هرم مستطيل طول ضلعه 10 سم وارتفاعه 12 سم فما مساحة سطح الهرم؟
إجابة:
معروف :
مساحة القاعدة = 10 × 10 = 100 سم 2
ارتفاع الهرم = 12 سم
مطلوب : مساحة الهرم
التسوية :
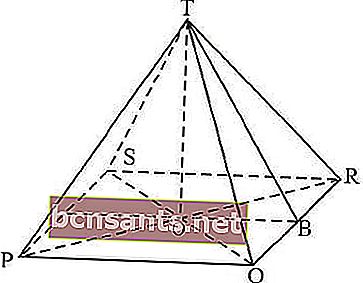
مساحة السطح = مساحة القاعدة + المساحة الكلية للجوانب الرأسية
مساحة القاعدة = الضلع × الضلع = 10 × 10 = 100 سم 2
المساحة الكلية للجانب العمودي = مساحة المثلث = 4 × مساحة المثلث QRT
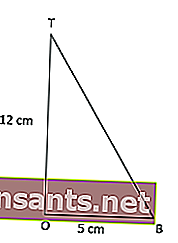
مع حساب فيثاغورس مثلث TOB ، يبلغ ارتفاع BT 13 سم. وبالتالي،
مساحة المثلث QRT = 1/2 × QR × BT = 1/2 × 10 × 13 = 65 سم 2
إجمالي مساحة الأضلاع الرأسية = 4 × مساحة المثلث QRT = 4 × 65 = 260
إذن ، مساحة سطح الهرم = 100 + 260 = 360 سم 2
مثال مشكلة 2.
تعلم أن مساحة قاعدة الهرم لشكل رباعي هي 16 سم 2 ، وارتفاع المثلث الرأسي 3 سم. أوجد مساحة سطح هرم المثلث.
إجابة.
من المعروف :
مساحة قاعدة الهرم = 16 سم 2
ارتفاع المثلث العمودي = 3 سم
مطلوب : مساحة الهرم
التسوية :
مساحة سطح الهرم = مساحة القاعدة + المساحة الكلية للجانب الرأسي
مساحة القاعدة = 16 سم 2
المساحة الكلية للشكل الرأسي = 4 × مساحة المثلث = 4 × (1/2 × 4 × 3) = 24 سم 2
إذن مساحة سطح الهرم = 16 + 24 = 40 سم 2
مثال مشكلة 3 .
هرم سداسي منتظم مساحة قاعدته 120 سم 2 ومساحته 30 سم 2 في مثلث قائم. أوجد مساحة سطح الهرم السداسي.
إجابة.
معروف:
مساحة القاعدة = 120 سم 2
مساحة المثلث العمودي = 30 سم 2
مطلوب : مساحة الهرم
التسوية :
مساحة السطح = مساحة القاعدة + المساحة الكلية للجوانب الرأسية
اقرأ أيضًا: تعرف على نظام الإخراج لدى البشر ووظائفهممساحة القاعدة = 120 سم 2
مساحة الأضلاع الرأسية = 6 × مساحة المثلثات الرأسية = 6 × 30 سم 2 = 180 سم 2
إذن ، مساحة سطح الهرم السداسي = 120 + 180 = 300 سم 2
صيغة حجم ليماس
تشتمل منطقة Limas على مساحة بناء بحيث يكون لها حجم. فيما يلي معادلة حجم الهرم بشكل عام.
حجم الهرم = 1/3 × مساحة القاعدة × الارتفاع
مثال على مشكلة تحديد حجم الهرم
لفهم استخدام صيغة حجم الهرم بشكل أفضل ، إليك بعض الأمثلة على مشاكل إيجاد حجم الهرم.
مثال مشكلة 1.
أوجد حجم هرم مثلث ضلع مساحة قاعدته 50 سم 2 وارتفاعه 12 سم.
إجابة.
معروف :
مساحة القاعدة = 50 سم 2
ارتفاع الهرم = 12 سم
المطلوب: حجم الهرم
التسوية :
حجم الهرم = 1/3 x مساحة القاعدة xt للهرم = 1/3 x 50 x 12 = 200 cm3
إذن ، حجم الهرم 200 سم 3
مثال مشكلة 2.
هرم مستطيل طول ضلعه 8 سم وارتفاع هرم 6 سم ما هو حجم الهرم؟
إجابة.
من المعروف :
جانب المستطيل = 8 سم
ارتفاع الهرم = 6 سم
المطلوب : حجم الهرم
التسوية :
حجم الهرم = 1/3 x مساحة القاعدة xt للهرم = 1/3 x (8 x 8) x 6 = 128 cm3
إذن ، حجم الهرم 128 سم 3.
مثال مشكلة 3.
من المعروف أن مساحة قاعدة الهرم 50 سم 2 وارتفاع الهرم 15 سم ، فما هو حجم الهرم؟
إجابة.
في المعرفة =
مساحة القاعدة = 50 سم 2
الارتفاع = 15 سم
طلب = حجم هرم خماسي
مستوطنة.
الحجم = 1/3 × مساحة القاعدة × الارتفاع
= 1/3 × 50 × 15
= 250 سم 3
إذن ، حجم الهرم 250 سم 3
وبالتالي ، شرح كامل لصيغة Limas: المساحة والحجم وعينة الأسئلة + المناقشة. ربما يكون مفيدا !
