مجموعة من الصيغ الرياضية للفئة 6 SD

تتكون المجموعة التالية من الصيغ الرياضية للصف السادس SD من:

مجموعة من صيغ الحجم لبناء المساحة وصيغة القياس
حساب المساحة المسطحة
عمليات عدد صحيح
صيغ عملية عد العدد الكسري
صيغة FPB و KPK هي رقمان
معالجة وتقديم البيانات
تنسيق صيغ النظام والحجم والوقت
جمع وطرح الكسور وتحديد الجذر التربيعي للأعداد التكعيبية.

الصنف 6 الصيغ الرياضية احسب حجم بناء غرفة

مساحة بناء الاسم	صيغ الحجم
الة النفخ	V = phi r² xt
مثلث بريما منتصب	V = مساحة القاعدة × الارتفاع

مقياس حساب مجموعة الصيغ الرياضية من الفئة 6

صيغ المقياس	= المسافة على الصورة (الخريطة) / المسافة الفعلية
صيغ المسافة في الشكل	= المسافة الفعلية × المقياس
صيغة المسافة الفعلية	= المسافة على الصورة (الخريطة) / المقياس

مجموعة من الصيغ لحساب مساحة الشقة

شخصية ثنائية الأبعاد	صيغة المنطقة
بناء مربع مسطح	L = الجانب x الضلع = s²
قم ببناء مثلث مسطح	L = ½ القاعدة × الارتفاع
بناء دائرة مسطحة	L = phi x r²
بناء شبه منحرف	L = ½ t × (أ + ب)
بناء طائرة ورقية مسطحة - طائرة ورقية	L = ½ xd ₁ xd ₂
بناء متوازي الأضلاع مسطح	L = القاعدة × الارتفاع
الحصول على ما يصل المعين المسطح	L = ½ xd ₁ xd ₂
بناء مستطيل مسطح	L = الطول × العرض

مجموعة من معادلات التشغيل الصحيح للفئة 6 SD

الخصائص التبادلية للإضافة ، الصيغ العامة: أ + ب = ب + أ

على سبيل المثال: 2 + 4 = 4 + 2 = 6 أو 5 + 10 = 10 + 5 = 15

الخصائص التبادلية لعملية الضرب ، الصيغ العامة: axb = bxa

على سبيل المثال: 3 × 5 = 5 × 3 = 15 أو 10 × 2 = 2 × 10 = 20

الخواص التوزيعية من الضرب إلى الجمع

الصيغة العامة: الفأس (ب + ج) = (المحور) + (الفأس)

مثال:

2 × (5 + 10)	= 2 × 5 + 2 × 10
	= 10 + 20
	= 30

الطبيعة التوزيعية من الضرب إلى الطرح

الصيغة العامة: الفأس (ب - ج) = (المحور) - (الفأس)

مثال:

2 × (10-5)	= 2 × 10-2 × 5
	= 20 + 10
	= 10

مجموعة من معادلات حساب العدد الكسري

عملية حساب الأعداد المختلطة لها شرطان ، من بين أمور أخرى:

اقرأ أيضًا: خصائص الكواكب في المجموعة الشمسية (FULL) بالصور والتفسيرات

أولاً ، إذا كان هناك أقواس () ، فافعل ما هو داخل الأقواس أولاً.

ثانيًا ، إذا لم يكن هناك أقواس () ، فقم بإجراء الضرب والقسمة أولاً ، ثم قم بإجراء عملية الجمع والطرح.

مثال:

= 7000 - 40 × 100: 4 + 200		= 1000: 10 × 2 - (200 + 50)
= 7000 - 1000 + 200		= 1000: 10 × 2 - 150
= 6200	أو	= 100 × 2 - 150
		= 200 - 150
		= 50

صيغة FPB و KPK هي رقمان

كيفية تحديد FPB (أكبر عامل مشترك) عددين ، من بين أمور أخرى ، أوجد العامل في كل من هذه الأرقام ، وتحديد العامل المشترك للرقمين وضرب العامل المشترك (نفس العامل) الذي لديه أصغر قوة.

مثال:

27	= 3³
18	= 2 × 3²

العامل المشترك لـ FPB في العددين هو 3 ، وأقل قوة هي 3² = 9

كيفية تحديد المضاعف المشترك الأصغر (المضاعف المشترك الأصغر) لرقمين ، من بين أمور أخرى ، ابحث عن العامل الأولي لكل رقم من هذه الأرقام ، واضرب جميع العوامل والعوامل المتشابهة ، أيهما أعلى رتبة.

على سبيل المثال: KPK قيم 12 و 15

12	= 2² × 3
15	= 3 × 5

قيمة المضاعف المشترك الأصغر رقمين أعلاه: 2 ² × 3 × 5 = 50

معالجة وتقديم البيانات

الوضع هو القيمة الأكثر ظهورًا.

الحد الأدنى للقيمة هو أصغر وأدنى قيمة لجميع البيانات.

القيمة القصوى هي أعلى قيمة لجميع البيانات الموجودة فيها.

يتم البحث عن المتوسط عن طريق جمع جميع العينات مقسومة على عدد العينات.

إيجاد نظام الإحداثيات
يُطلق على المحور السيني أيضًا اسم Absis (x) وبالنسبة للمحور y يُطلق عليه أيضًا اسم Ordinate (y).
سيتم تشكيل مستوى الإحداثيات الديكارتية بواسطة محورين ، وهما المحور القائم (المحور الصادي) والمحور الأفقي (المحور السيني).
من نقطة الصفر ، سيكون المحور الرأسي صاعدًا وسيكون المحور الأفقي على اليمين والذي له قيمة موجبة.
من نقطة الصفر ، سينخفض المحور الرأسي إلى الأسفل وسيتجه المحور الأفقي إلى اليسار الذي له قيمة سالبة.
يمكن العثور على إحداثيات كائن عن طريق إيجاد الموقع على المحور x إلى اليمين أو اليسار مع تحديد الموضع على المحور y لأعلى أو لأسفل.

اقرأ أيضًا: أسئلة الرياضيات للصف السادس (+ مناقشة) SD UASBN - كاملة

علاقة وحدة الحجم

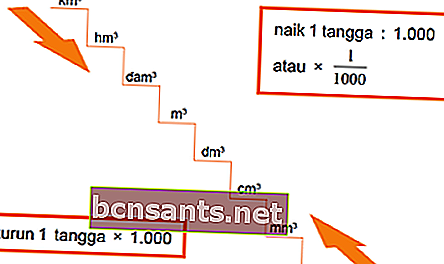
مثال:

1 كم 3 = 1000 سم مكعب (أسفل سلم واحد)

1 م 3 = 1،000،000 سم 3 (نزول درجين)

1 م 3 = 1/1000 دم 3 (فوق سلم واحد)

1 م 3 = 1 / 1،000،000 hm3 (حتى درجين)

الحجم باللترات

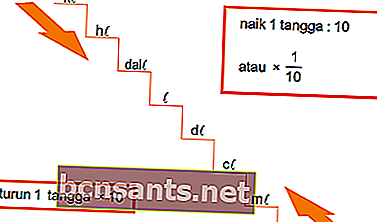
الوحدة الزمنية

دقيقة واحدة	= 60 ثانية
ساعة واحدة	= 60 دقيقة
يوما ما	= 24 ساعة
اسبوع واحد	= 7 أيام
شهر واحد	= 30 يومًا / 31 يومًا
شهر واحد	= 4 أسابيع
سنة واحدة	= 52 أسبوعًا
سنة واحدة	= 12 شهر
واحد Windu	= 8 سنوات
عقد واحد	= 10 سنوات
عقد واحد	= 10 سنوات
قرن واحد	= 100 سنة
الألفية واحدة	= 1000 سنة

ثواني التحويل

1 دقيقة = 60 ثانية
1 ساعة = 3600
1 يوم = 86400
شهر واحد = 2592000 ثانية
سنة واحدة = 31104000 ثانية

جمع وطرح الكسور

لتتمكن من جمع الكسور وطرحها ، يجب أولاً تسوية المقامات.

مثال:

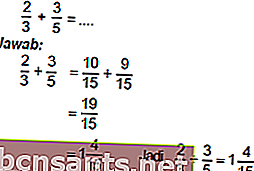
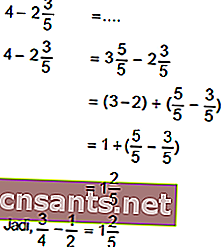
ضرب وقسمة الكسور

من السهل جدًا ضرب الكسور. ضرب البسط في البسط. ضرب المقام في المقام. إذا كان من الممكن تبسيطها ، فقم بالتبسيط:

القسمة الكسرية هي نفسها الضرب في مقسوم الكسر.

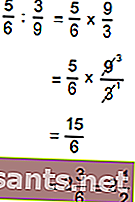
أوجد الجذر التكعيبي لعدد مكعب

يتم قراءة 13 كقوة ثلاثة = 1 × 1 × 1 = 1

يُقرأ 23 على أنه اثنان أس ثلاثة = 2 × 2 × 2 = 8

يُقرأ 33 على شكل ثلاثة مكعبات = 3 × 3 × 3 = 27

يُقرأ 43 على أنه أربعة أس ثلاثة = 4 × 4 × 4 = 64

يُقرأ 53 على أنه خمسة أس ثلاثة = 5 × 5 × 5 = 125

1 ، 8 ، 27 ، 64 ، 125 وما إلى ذلك هي أعداد أو قوى مكعبة 3

جمع وطرح

23 + 33 = (2 × 2 × 2) + (3 × 3 × 3)

= 8 + 27

= 35

63-43 = (6 × 6 × 6) - (4 × 4 × 4)

= 216 - 64

= 152

الضرب والقسمة

23 × 43 = (2 × 2 × 2) × (4 × 4 × 4)

= 8 × 64

= 512

63:23 = (6 × 6 × 6): (2 × 2 × 2)

= 216: 8

= 27

هذه مجموعة من معادلات الرياضيات للمدرسة الابتدائية للصف السادس والتي تظهر غالبًا في أسئلة الاختبار النهائي الوطني (UAN) والامتحان الوطني (الأمم المتحدة). ربما يكون مفيدا.