أكمل الجدول المثلثي Sin Cos Tan (كل الزوايا) + كيفية فهمه

الجدول المثلثي sin cos tan عبارة عن سلسلة من الجداول التي تحتوي على القيمة المثلثية أو sin tangent لزاوية.

تعرض هذه المقالة جدولًا للقيم المثلثية لـ sin cos tan من زوايا خاصة مختلفة من 0º إلى 360º (أو ما يُعرف عمومًا بزاوية الدائرة 360 درجة) ، بحيث لا تحتاج إلى عناء حفظها بعد الآن.

بالنسبة لصيغة الهوية المثلثية ، يمكنك قراءتها في هذا المقال.

تعريف Sin Cos Tan

قبل الدخول في جدول القيم المثلثية ، يساعدنا ذلك في فهم المصطلحات حساب المثلثات وجيب cos tan.

• علم المثلثات هو فرع من فروع الرياضيات يدرس العلاقة بين طول وزاوية المثلث.
• sin (sine) هي نسبة الطول في المثلث بين مقدمة الزاوية والوتر ، y / z.
• كوس (جيب التمام) هو نسبة الطول في المثلث بين ضلع الزاوية والوتر ، x / z.
• تان (الظل) هي نسبة أطوال المثلث بين مقدمة الزاوية والضلع ، ص / س.

تقتصر جميع المقارنات المثلثية لـ tan sin cos على المثلثات القائمة الزاوية أو المثلثات بزاوية 90 درجة فقط.

الربع الأول جدول قياس الزوايا الخاص (0-90 درجة)

ركن	0 º	30 º	45 º	60 º	90 º
الخطيئة	0	1/2	1/2 √2	1/2 √3	1
كوس	1	1/2 √3	1/2 √2	1/2	0
تان	0	1/2 √3	1	√3	∞

جدول قياس الزاوية الخاصة للربع الثاني (90-180 درجة)

ركن	90 º	120 º	135 º	150 º	180 º
الخطيئة	1	1/2 √3	1/2 √2	1/2	0
كوس	0	- 1/2	- 1/2 √2	- 1/2 √3	-1
تان	∞	-√3	-1	- 1/3 √3	0

جدول الزاوية الخاصة رباعي الزاوية III من Sin Cos Tan (180-270 درجة)

ركن	180 º	210 º	225 º	240 º	270 º
الخطيئة	0	- 1/2	- 1/2 √2	- 1 / 2√3	-1
كوس	-1	- 1 / 2√3	- 1 / 2√2	- 1/2	0
تان	0	1/3√3	1	√3	∞

Cos Sin Tan Table Special Angle Quadrant IV (270 - 360 درجة)

ركن	270 º	300 º	315 º	330 º	360 درجة
الخطيئة	-1	-½√3	-½√2	-½	0
كوس	0	½	½√2	½√3	1
تان	∞	-√3	-1	-1 / 3√3	0

وبالتالي قائمة كاملة بالجداول المثلثية من جميع الزوايا الخاصة من 0 - 360 درجة.

اقرأ أيضًا: عملية آلية الرؤية البشرية ونصائح العناية بالعيون

يمكنك استخدام هذا الجدول لتسهيل الأعمال في حساب أو تحليل علم المثلثات في الرياضيات.

تذكر الزاوية الخاصة المثلثية الجدول بدون حفظ

في الواقع ، ليس عليك أن تكلف نفسك عناء حفظ كل القيم المثلثية من كل زاوية.

كل ما تحتاجه هو مفهوم فهم أساسي يمكنك استخدامه لمعرفة القيمة المثلثية لأي زاوية معينة.

تحتاج فقط إلى تذكر مكونات طول ضلع المثلث عند الزوايا الخاصة 0 و 30 و 45 و 60 و 90 درجة.

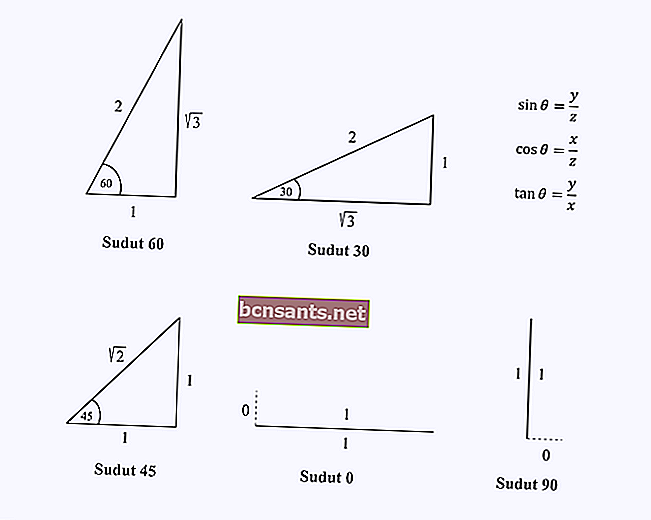
افترض أنك تريد إيجاد قيمة cos (60).

ما عليك سوى تذكر طول ضلع المثلث بزاوية 60 درجة ، ثم إجراء عملية جيب التمام ، وهي x / z على هذا المثلث.

من الشكل ، سترى أن قيمة cos 60 = 1/2.

قراءة سهلة؟

بالنسبة للزوايا في الأرباع الأخرى ، فإن الطريقة هي نفسها وتحتاج فقط إلى تعديل الإشارة الموجبة أو السلبية لكل ربع.

الجدول في شكل دائرة

إذا كان جدول cos sin tan أعلاه طويلًا جدًا بحيث لا يمكن تذكره ، وأيضًا إذا كانت طريقة مفهوم الزاوية الخاصة التي تعتقد أنها لا تزال صعبة ...

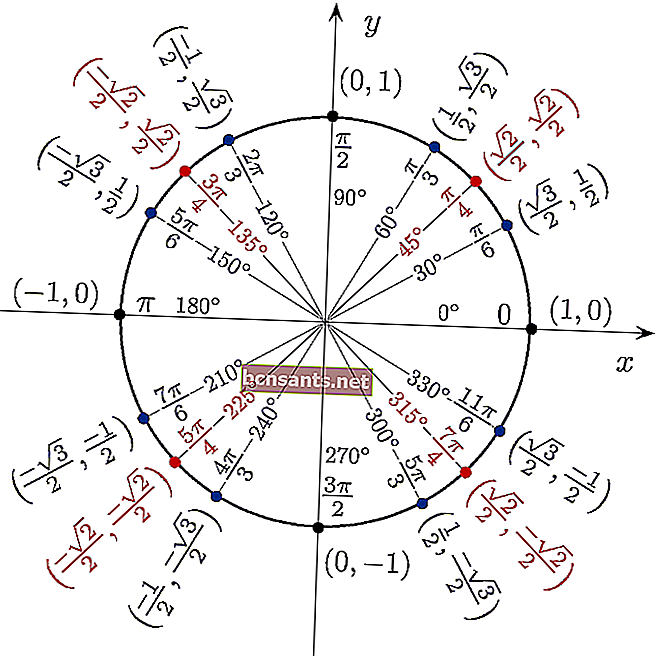
يمكنك استخدام الجدول المثلثي في ​​شكل دائرة لترى مباشرة قيمة sin cos tan من زاوية 360 درجة.

حيل سريعة لحفظ الجداول المثلثية

بالإضافة إلى الطرق المذكورة أعلاه ، هناك طريقة أخرى يمكنك استخدامها لتذكر جداول الصيغ المثلثية بسهولة.

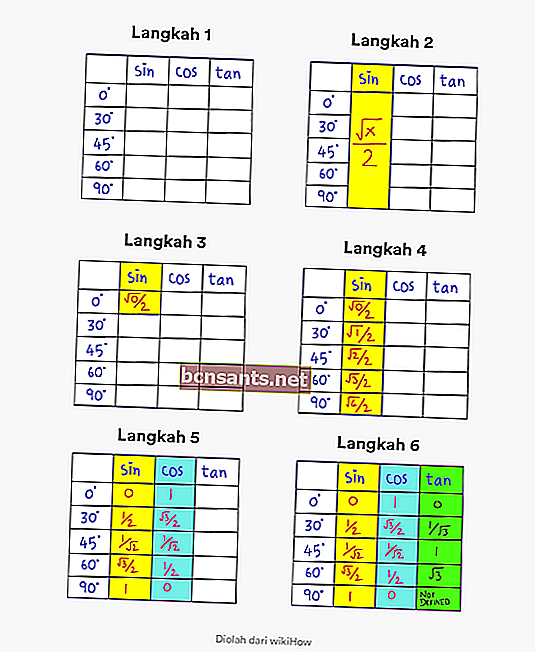
الخطوات التي عليك القيام بها هي كما يلي:

• الخطوة 1 . أنشئ جدولاً يحتوي على زوايا من 0 إلى 90 درجة وأعمدة بالوصف sin cos tan
• الخطوة الثانية . لاحظ أن الصيغة العامة لجيب بزاوية 0-90 درجة هي √x / 2.
• الخطوة 3 . قم بتغيير قيمة x إلى 0 في √x / 2 في العمود الأول. الزاوية اليسرى في الاعلى.
• الخطوة 4. املأ التسلسل بتغيير x إلى 0 ، 1 ، 2 ، 3 ، 4 في عمود الخطيئة. وهكذا تكون قد حصلت على القيمة المثلثية الكاملة sin
• الخطوة الخامسة . للعثور على قيمة cos ، كل ما عليك فعله هو عكس الترتيب في عمود sin.
• الخطوة 6 . لإيجاد قيمة tan ، كل ما عليك فعله هو قسمة قيمة sin على قيمة cos.

اقرأ أيضًا: القصص الخيالية: أمثلة ، تعريف وعناصر [FULL

أيهما يسهل عليك فهمه عند تذكر القيمة المثلثية لـ tan sin cos؟

في كلتا الحالتين ، اختر الطريقة التي يسهل عليك فهمها. لأن كل شخص لديه أسلوب تعلم مختلف.

جداول لجميع الزوايا

إذا كانت القيم الموضحة في الجداول أعلاه هي القيم المثلثية للزوايا الخاصة فقط ، فإن هذا الجدول يعرض جميع القيم المثلثية لجميع الزوايا من 0 إلى 90 درجة.

ركن	راديان	الخطيئة	كوس	تان
0 درجة	0	0	1	0
1 درجة	0.01746	0.01746	0.99985	0.01746
2 درجة	0.03492	0.03491	0.99939	0.03494
3 درجة	0.05238	0.05236	0.99863	0.05243
4 درجات	0.06984	0.06979	0.99756	0.06996
5 درجات	0.0873	0.08719	0.99619	0.08752
6 درجة	0.10476	0.10457	0.99452	0.10515
7 درجة	0.12222	0.12192	0.99254	0.12283
8 درجة	0.13968	0.13923	0.99026	0.1406
9 درجة	0.15714	0.1565	0.98768	0.15845
10 درجة	0.1746	0.17372	0.9848	0.1764
11 درجة	0.19206	0.19089	0.98161	0.19446
12 درجة	0.20952	0.20799	0.97813	0.21265
13 درجة	0.22698	0.22504	0.97435	0.23096
14 درجة	0.24444	0.24202	0.97027	0.24943
15 درجة	0.26191	0.25892	0.9659	0.26806
16 درجة	0.27937	0.27575	0.96123	0.28687
17 درجة	0.29683	0.29249	0.95627	0.30586
18 درجة	0.31429	0.30914	0.95102	0.32506
19 درجة	0.33175	0.32569	0.94548	0.34448
20 درجة	0.34921	0.34215	0.93965	0.36413
21 درجة	0.36667	0.35851	0.93353	0.38403
22 درجة	0.38413	0.37475	0.92713	0.40421
23 درجة	0.40159	0.39088	0.92044	0.42467
24 درجة	0.41905	0.40689	0.91348	0.44543
25 درجة	0.43651	0.42278	0.90623	0.46652
26 درجة	0.45397	0.43854	0.89871	0.48796
27 درجة	0.47143	0.45416	0.89092	0.50976
28 درجة	0.48889	0.46965	0.88286	0.53196
29 درجة	0.50635	0.48499	0.87452	0.55458
30 درجة	0.52381	0.50018	0.86592	0.57763
31 درجة	0.54127	0.51523	0.85706	0.60116
32 درجة	0.55873	0.53011	0.84793	0.62518
33 درجة	0.57619	0.54483	0.83854	0.64974
34 درجة	0.59365	0.55939	0.8289	0.67486
35 درجة	0.61111	0.57378	0.81901	0.70057
36 درجة	0.62857	0.58799	0.80887	0.72693
37 درجة	0.64603	0.60202	0.79848	0.75396
38 درجة	0.66349	0.61587	0.78785	0.78172
39 درجة	0.68095	0.62953	0.77697	0.81024
40 درجة	0.69841	0.643	0.76586	0.83958
41 درجة	0.71587	0.65628	0.75452	0.86979
42 درجة	0.73333	0.66935	0.74295	0.90094
43 درجة	0.75079	0.68222	0.73115	0.93308
44 درجة	0.76825	0.69488	0.71913	0.96629
45 درجة	0.78571	0.70733	0.70688	1،00063
46 درجة	0.80318	0.71956	0.69443	1.0362
47 درجة	0.82064	0.73158	0.68176	1.07308
48 درجة	0.8381	0.74337	0.66888	1.11137
49 درجة	0.85556	0.75494	0.6558	1.15117
50 درجة	0.87302	0.76627	0.64252	1.1926
51 درجة	0.89048	0.77737	0.62904	1،2358
52 درجة	0.90794	0.78824	0.61537	1.28091
53 درجة	0.9254	0.79886	0.60152	1.32807
54 درجة	0.94286	0.80924	0.58748	1.37748
55 درجة	0.96032	0.81937	0.57326	1.42932
56 درجة	0.97778	0.82926	0.55887	1.48382
57 درجة	0.99524	0.83889	0.5443	1.54122
58 درجة	1.0127	0.84826	0.52957	1.60179
59 درجة	1.03016	0.85738	0.51468	1.66584
60 درجة	1.04762	0.86624	0.49964	1،73374
61 درجة	1.06508	0.87483	0.48444	1.80587
62 درجة	1.08254	0.88315	0.46909	1.8827
63 درجة	1.1	0.89121	0.4536	196476
64 درجة	1.11746	0.89899	0.43797	2.05265
65 درجة	1.13492	0.9065	0.4222	2.14707
66 درجة	1.15238	0.91373	0.40631	2.24884
67 درجة	1.16984	0.92069	0.3903	2.35894
68 درجة	1.1873	0.92736	0.37416	2.4785
69 درجة	1.20476	0.93375	0.35792	2.60887
70 درجة	1.22222	0.93986	0.34156	2.75169
71 درجة	1.23968	0.94568	0.3251	2.90892
72 درجة	1.25714	0.95121	0.30854	3.08299
73 درجة	1.2746	0.95646	0.29188	3.27686
74 درجة	1.29206	0.96141	0.27514	3،49427
75 درجة	1.30952	0.96606	0.25831	3.73993
76 درجة	1.32698	0.97043	0.2414	4.01992
77 درجة	1.34444	0.97449	0.22442	4.34219
78 درجة	1.36191	0.97826	0.20738	4،71734
79 درجة	1.37937	0.98173	0.19026	5.15984
80 درجة	1.39683	0.98491	0.1731	5.68998
81 درجة	1.41429	0.98778	0.15587	6.33709
82 درجة	1.43175	0.99035	0.1386	7.14523
83 درجة	1.44921	0.99262	0.12129	8.18379
84 درجة	1.46667	0.99458	0.10394	956868
85 درجة	1.48413	0.99625	0.08656	115092
86 درجة	1.50159	0.99761	0.06915	14،4259
87 درجة	1.51905	0.99866	0.05173	193069
88 درجة	1.53651	0.99941	0.03428	29153
89 درجة	1.55397	0.99986	0.01683	59.4189
90 درجة	1.57143	1	0	∞

نأمل أن يكون هذا التفسير المثلثي مفيدًا لك.

ستكون هذه المادة ذات فائدة كبيرة لمجموعة متنوعة من التطبيقات في الرياضيات والفيزياء المتقدمة.

يمكنك أيضًا تعلم مواد مدرسية أخرى في Saintif ، مثل الأعداد الأولية وتحويلات الوحدات والصيغ المستطيلة وما إلى ذلك.

مرجع

• علم المثلثات - ويكيبيديا
• أدوات الرياضيات - علم المثلثات